Некоторые применения трехмерной клеточно–автоматной модели потока вязкой жидкости RD-I

Институт вычислительной математики и математической геофизики СО РАН, Новосибирск

Ю.Г. Медведев
© 2005

Введение

Клеточно-автоматное (КА) моделирование потоков жидкости в последнее время получило большое развитие. Известен ряд двумерных моделей, а также четырехмерная модель, моделирующая трехмерные потоки [1]. В [2] была предложена трехмерная КА модель, называемая RD-I, имеющая гораздо меньшую сложность, чем четырехмерная модель. Результаты экспериментальных исследований [3] подтверждают, что модель RD-I действительно моделирует поток вязкой жидкости. Количественные характеристики параметров потока получены в [4]. Соотношения между модельными и физическими характеристиками потока, такими как вязкость, геометрические размеры, давление приведены в [5].

В работе кратко рассмотрена модель RD-I, приведены соотношения физических и модельных величин и описаны проведенные с ней эксперименты по моделированию потока в трубе и в пористой среде, а также эксперименты с параллельной версией программной реализации.

Краткое описание модели RD-I

КА моделирует потоки жидкости следующим образом. В клетках находятся некоторые гипотетические частицы. Их масса и скорость единичны, количество возможных направлений вектора скорости совпадает с числом соседних клеток, а правила движения выбраны так, чтобы выполнялись законы сохранения массы и импульса. Каждый такт работы КА разбит на две фазы: столкновение и сдвиг. На фазе столкновения происходит изменение направления движения частиц согласно некоторым законам столкновения. На фазе сдвига каждая частица перемещается в соответствующую ее вектору скорости соседнюю клетку.

Рассматриваемая в работе трехмерная КА модель является приближенной моделью потока. Каждая клетка автомата, используемого в этой модели, имеет 12 соседей. Это значительно меньше, чем у других трехмерных КА моделей [1], что обуславливает сравнительно малые затраты машинного времени при моделировании. Клетки рассматриваемого КА имеют форму ромбических додекаэдров. Если заполнить трехмерное пространство этими многогранниками с единичным расстоянием между двумя противолежащими гранями, то координаты клеток автомата совпадут с координатами центров додекаэдров. При этом соседние клетки будут находиться в центрах додекаэдров, имеющих общую грань.

Состояние каждой клетки автомата может быть описано булевым вектором s=(s₁, s₂, ..., s₁₃), s_i принадлежит {0, 1}, каждый компонент которого s_i указывает на наличие или отсутствие в клетке частицы с определенным вектором скорости. Количество возможных векторов скорости частиц равно количеству соседних клеток. В клетке не может быть более одной частицы с одинаковыми векторами скорости. Следовательно, длина вектора s равна сумме количества соседей и количества частиц покоя (частиц с нулевым вектором скорости). В Декартовой системе координат КА расположен таким образом, что углы между направлениями векторов скорости частиц и координатными осями составляют либо 90^o, либо 45^o. Поэтому проекции единичных векторов на оси равны либо 0, либо 0.707 соответственно.

В различных модификациях модели возможны различные варианты правил столкновения, но во всех случаях, должны выполняться законы сохранения массы и импульса при каждом столкновении. В описанных ниже экспериментах использовался полный набор правил с одной частицей покоя. Так как в структуре решетки модели 12 соседей и одна частица покоя, то число входных состояний будет 2¹³. Каждому i-му из этих 8192 входных состояний таблицы переходов автомата соответствуют все такие выходные состояния, у которых суммарные масса и импульс частиц в клетке не изменялись бы при столкновении. Эти наборы из n_i выходных состояний (i = 1, 2, … , 8192) и приняты за правила столкновения с вероятностью срабатывания каждого варианта 1/n_i, где n_i принимает значения от 1 до 56.

Одно из преимуществ КА–моделей — это простые граничные условия. Они определяются введением в модель дифференциации клеток по типам. При моделировании течения жидкости можно выделить следующие типы клеток: рабочая клетка, клетка-стенка и клетка-источник частиц. У всех клеток одного типа одинаковые функции переходов. У клеток разных типов — разные. Фаза сдвига всех типов клеток происходит одинаково, различия поведения есть только на фазе столкновения.

Функции переходов клеток стенки отличаются от функции переходов рабочих клеток таким образом, чтобы векторы скорости частиц изменялись по законам, обеспечивающим отражающие функции стенки. Для стенок с трением законом отражения является изменение всех векторов скорости частиц на противоположные. Именно такие стенки были использованы в экспериментах, описанных ниже.

Каждая клетка–источник с некоторой вероятностью генерирует частицы со всевозможными направлениями вектора скорости. Установив такие клетки в пространстве в одну линию, мы получим источник равномерного потока частиц. Изменяя вероятность рождения частиц, мы можем варьировать интенсивность потока.

Следует заметить, что при моделировании потоков наибольший интерес представляют не столько сами гипотетические частицы клеточного автомата с их скоростями движения, сколько осредненные для каждой точки значения их скоростей u и концентраций n в некоторой окрестности радиуса r. Осредненная скорость получается как сумма всех векторов частиц в области осреднения. Именно она и сопоставляется с макроскопической скоростью реальной жидкости. Осредненная концентрация подсчитывается как среднее по области осреднения количество частиц.

Важными параметрами КА моделей потоков являются модельная вязкость v_мод и структурный коэффициент g, вносящий поправку на дискретность модели. Методика их вычисления для всего класса КА моделей потоков жидкости описана в [6]. В [4] общее выражение приводится к виду, применимому для модели RD-I с 12 соседями. Значения коэффициента g также были вычислены для плотностей от 0.25 до 12.75 с шагом 0.25.

Таким образом, основываясь на теоретических выкладках, справедливых для всех КА моделей потоков, были вычислены модельная вязкость v и структурный коэффициент g для исследуемой модели.

При использовании модели для моделирования реальных физических задач необходимо иметь аппарат, позволяющий переводить задаваемые в реальных физических величинах граничные условия в модельные величины, а получившиеся результаты из модельных величин обратно в физические. Модельные величины, описанные в предыдущем параграфе, связаны между собой теми же законами физики, что и реальные физические величины, им соответствующие. Из этих законов получаются соотношения, связывающие физические и модельные параметры, которые используются в большинстве известных КА моделях.

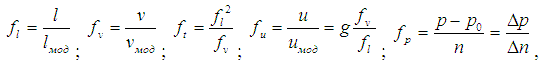
где l, v, u, p – физические длина, вязкость, скорость и давление соответственно, l_мод, v_мод, u_мод, n – модельные длина, вязкость, скорость и концентрация частиц, f_l, f_v, f_u, f_t, f_p – коэффициенты, связывающие физические параметры с модельными.

Экспериментальное исследование модели RD-I

Серия экспериментов по моделированию потока вязкой жидкости в трубе круглого сечения была поставлена для того, чтобы подтвердить соответствие модели реальному потоку, скорость которого в трубе можно рассчитать аналитически из закона Пуазейля. Клеточный автомат имеет форму прямоугольного параллелепипеда размером 101x101x2000 клеток, ориентированного вдоль осей X, Y и Z соответственно. В нем клетками стенки ограничен круговой цилиндр радиусом 50 клеток. На одной из перпендикулярных оси цилиндра граней параллелепипеда выстроена плоскость из клеток – источников частиц. Каждая из этих клеток на каждой итерации с заданной вероятностью может генерировать частицы со всеми возможными направлениями векторов скорости. Аналитически рассчитанное распределение скорости потока в поперечном сечении трубы представляет собой параболоид в соответствии с законом Пуазейля [7]. Параболоид получается и экспериментально. На рис. 1 приведено меридианное сечение этого параболоида, полученное при осреднении с радиусами от r = 1 до r = 10 клеток. Из рисунка видно, что при малых радиусах осреднения автоматный шум недопустимо большой. Радиуса r = 10 клеток вполне хватает, чтобы уровень автоматного шума находился в пределах приемлемой величины.

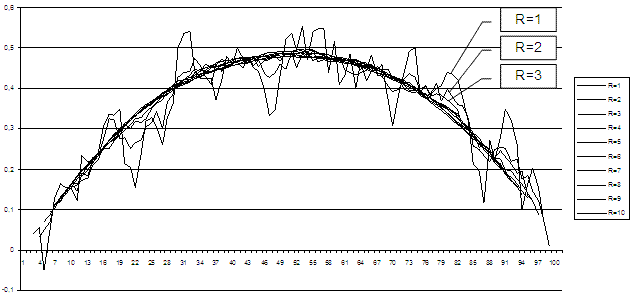
Рис. 1. Скорость потока жидкости в трубе при разных радиусах осреднения

Значения по оси абсцисс – расстояние от стенки трубы вдоль ее диаметра (в модельных единицах), по оси ординат – величина осредненного вектора скорости (в модельных единицах, нормированных на количество клеток, участвовавших в осреднении). Кривые получены при осреднении с радиусами от 1 до 10 клеток в сечении Z=1000 после 300 тысяч итераций.

В следующем эксперименте производилось построение зависимости скорости потока в пористой среде от разности давлений на концах участка. Параметры эксперимента были следующие. Размер автомата 800?50?800 клеток. Границы участка, на котором измерялась концентрация модельных частиц, z₁ = 100 клеток, z₂ = 700 клеток. Радиус сферических областей r_сф = 5 клеток, количество областей n_сф = 16000. Плотность заполнения r_пор = 19.8 %. Количество итераций — 150 тысяч. Для изменения концентрации частиц производилась генерация частиц клетками – источниками с разной вероятностью, что давало различную концентрацию модельных частиц. Зависимость скорости потока от концентрации получилась линейной. Из гидродинамики известен закон Дарси, который определяет зависимость скорости движения жидкости в пористой среде от давления: U = k(i – i₀), где U – скорость просачивания, k – коэффициент фильтрации, i = p/l – напорный градиент (p – градиент давления жидкости на участке длины l), а i₀ – пороговый напорный градиент, определяемый минимальным давлением, при котором начинается фильтрация. Так как концентрация модельных частиц связана с давлением моделируемой жидкости линейно, то получившаяся экспериментальная зависимость (рис. 2) аппроксимирует закон Дарси. Это позволяет заключить, что модель RD-I моделирует потоки жидкости с граничными условиями большой сложности, в том числе и в пористой среде.

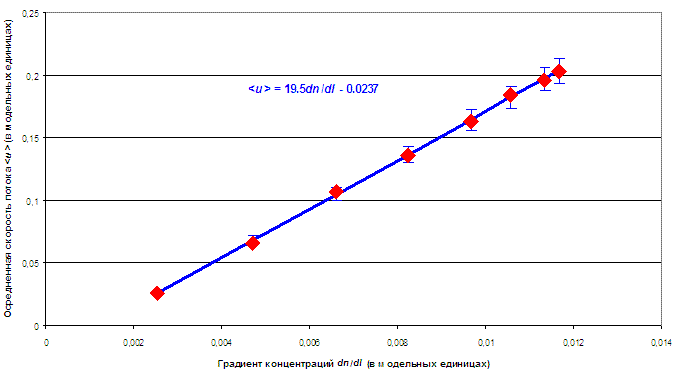
Рис. 2. Закон Дарси и экспериментальные данные

Значения по оси абсцисс – напорный градиент (в модельных единицах), по оси ординат – величина осредненного вектора скорости (в модельных единицах, нормированных на количество клеток, участвовавших в осреднении). Прямая теоретически рассчитана по закону Дарси. Экспериментальные значения, обозначенные точками, получены после 300 тысяч итераций.

Экспериментальное исследование эффективности распараллеливания производилось на кластере МВС-1000/М, принадлежащем Межведомственному суперкомпьютерному центру (МСЦ, Москва). КА, использованный в этих экспериментах, имел размер 2000x2000x101 клеток и разрезался на различное количество процессоров вдоль оси X (2000 клеток). При этом измерялась зависимость времени работы симулятора от количества процессоров. Кластер МСЦ имеет 512 процессоров DEC Alpha 21264 (633 МГц): 12 стоек по 16 двухпроцессорных модулей, соединенных сетью Myrinet. Измерено время вычислений 100 итераций на количестве процессоров от n_p = 1 до n_p = 384 с переменным шагом, из которого вычислено ускорение вычислений и эффективность распараллеливания, приведенная на рис. 3. Эффективность распараллеливания в пределах одной стойки (32 процессора) получилась более 90 %, а в пределах кластера (более 32 процессоров) — порядка 60 %. Падение производительности при n_p > 32 объясняется многокаскадной структурой сети кластера.

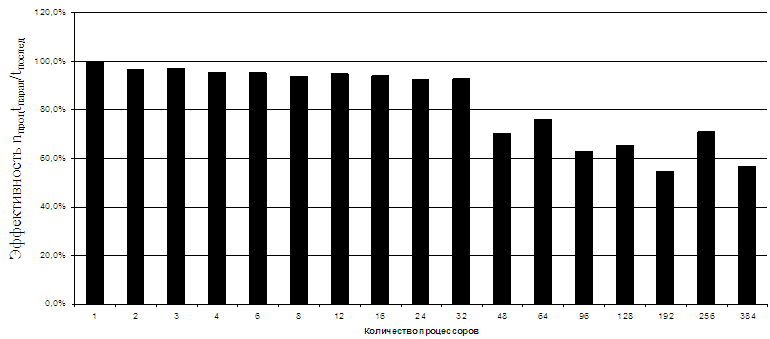
Рис. 3. Эффективность распараллеливания (Кластер МСЦ)

Значения по оси абсцисс – количество процессоров n_проц, по оси ординат – эффективность распараллеливания n_процt_парал/t_послед., где t_парал – время вычислений на nпроц, процессорах, t_послед – время вычислений на одном процессоре.

Заключение

На основании законов, общих для всех КА моделей потоков, вычислены параметры трехмерной КА модели потока жидкости RD-I. Из этих параметров получены соотношения модельных и физических величин. На основании экспериментов показано соответствие поля скорости потока жидкости в трубе с аналитически рассчитанным по закону Пуазейля. Установлено соответствие результатов моделирования пористой среды при помощи RD-I закону Дарси. Таким образом, модель RD-I позволяет решать задачи с граничными условиями большой сложности без дополнительных затрат машинного времени. Кроме того, достигнута высокая эффективность распараллеливания программной реализации модели RD-I.

Список литературы

1. U. Frisch a et al. Lattice Gas Hydrodynamics in Two and Three Dimensions. // Complex Systems, v. 1, 1987. P 649-707.

2. Ю.Г.Медведев. Трехмерная клеточно-автоматная модель потока вязкой жидкости. // Автометрия, т.39, N 3, 2003, С. 43 – 50.

3. Ю.Г.Медведев. Моделирование трехмерных потоков клеточными автоматами. // Вестник Томского Государственного университета N1(II), Приложение, Томск, изд-во ТГУ, 2002. С. 236 – 240.

4. Ю.Г.Медведев. Вычислительные эксперименты по определению связи физических величин с параметрами трехмерной КА–модели потока жидкости. // Труды конференции молодых ученых ИВМиМГ, Новосибирск, 2004.

5. Ю.Г.Медведев. Соотношение модельных и физических величин для трехмерной клеточно–автоматной модели потока жидкости. // Вестник Томского Государственного университета, Приложение, Томск, изд-во ТГУ, 2004.

6. Daniel H. Rothman, Stephane Zaleski. Lattice–Gas Cellular Automata. / Cambridge University Press, 1997. — 298 p.

7. Лойцянский Л.Г. Механика жидкости и газа. — М.: Наука. 1987. — 840 с.