© 2003
Кузнецов Б.П.
Исходный текст программы к статье (~17 кб)
Однажды автор решил провести вычислительный эксперимент с моделью конечного автомата (RS-триггером), заменяя дискретные двоичные переменные на непрерывные, изменяющиеся в нормированном диапазоне от нуля до единицы, а знаки логических операций И, ИЛИ, НЕ - на знаки арифметических операций: умножение, сложение и дополнение до единицы, соответственно. В результате проб и ошибок получилась новая математическая модель, изображенная на рис. 1, названная экспоненциальным триггером, так как компьютерное моделирование показало, что данная модель регистрирует приращения входных переменных в соответствии с экспоненциальной зависимостью от времени. Для краткости данную модель будем именовать Э-триггером.
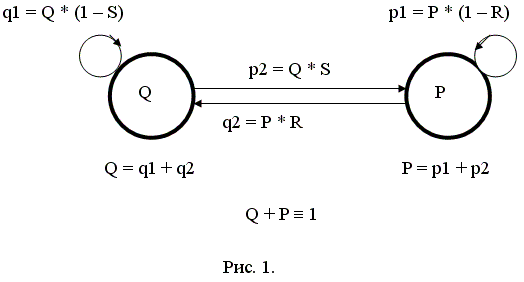
На рис. 1 изображена диаграмма состояний (граф переходов) Э-триггера. Граф содержит две вершины: Р – соответствует состоянию Э-триггера, изменяющего свое значение в непрерывном диапазоне от нуля до единицы; Q – дополнению до единицы (инверсия) этого состояния Р. Дуга и петля, заходящие в одну вершину, каждая вносит свою лепту (приращение) в итоговое на данный момент (дискретного) времени значение соответствующего вершине состояния. Так, например, значение Р складывается из двух компонент p1 и p2. При этом компонента p1 определяет влияние возрастающего значения переменной R (вход сброса Э-триггера) на убывание значения Р, в то время, как компонента p2 определяет влияние возрастающего значения переменной S (вход установки Э-триггера) на возрастание значения P. Формулы вычисления компонент представлены на том же рисунке.
На основе представленного графа переходов составлена следующая система уравнений
|
(1) |
P(t) = P(t-1) * (1 – R(t-1)) + Q(t-1) * S(t-1), |
|
|
Q(t) = Q(t-1) * (1 – S(t-1)) + P(t-1) * R(t-1). |
В формулах (1) используются обычные арифметические операции, включая умножение (знак «*»).
Функционирование Э-триггера на базе вычислений в соответствии с (1) можно представить в табличном виде, однако объем такой таблицы достаточно велик. Поэтому ограничимся формульными и графическими пояснениями.
Покажем, что функционирование Э-триггера описывается экспоненциальной зависимостью значения состояния Р от модельного времени t:
|
(2) |
P = Po * exp( - (R + S) * t ) + S / (R + S). |
В приведенной формуле Po – начальное значение состояния Э-триггера, exp(х) – экспонента, то есть основание натурального логарифма в степени х. При этом предполагается, что
Po > S / (R + S).
Подставляя в (1) значение Q, вычисленное через Р, то есть
Q = 1 – P (рис. 1), получим
|
(3) |
P(t+1) = P(t) * (1 – R(t)) + (1 – P(t)) * S(t). |
Это выражение после упрощения и опускания индексов при R и S принимает следующий вид
|
(4) |
P(t+1) – P(t) = - P(t) * (R + S) + S. |
Считая единичным приращение h времени, дополним правую часть полученного уравнения следующим образом:
|
(5) |
P(t+h) – P(t) = (- P(t) * (R + S) + S) * h. |
Полагая h > 0, разделим обе части уравнения на h:
|
(6) |
( P(t+h) – P(t) ) / h = - P(t) * (R + S) + S. |
Полученное выражение (при h -> 0) есть формула Эйлера для приближенного решения задачи Коши вида
|
(7) |
P' = - (R + S) * P + S, |
где P' – производная P по времени, P(0) = Po – начальное значение P в момент начала отсчета времени.
В начале положим S = 0, тогда (7) принимает вид
Это уравнение имеет следующее решение:
|
(8) |
P = Po * exp(- R * t), |
Из этого выражения следует, что при Po > 0 (при воздействии на Э-триггер некоторой величины R > 0 и при S = 0), его состояние изменяется по ниспадающей экспоненте. Будем искать решение уравнения (7) также в виде экспоненциальной зависимости вида
где k = - (R + S). Возьмем производную данной функции
|
|
P' = U' * exp(k * t) + U * k * exp(k * t) |
и сопоставим ее с выражением (7), заменяя P на (9):
|
|
U' * exp(k * t) + U * k * exp(k * t) = U * k * exp(k * t) + S. |
После приведения подобных получим:
Из данного выражения следует
|
(10) |
U' = S * exp( - k * t). |
Обозначив 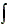 знак неопределенного интеграла, получим знак неопределенного интеграла, получим
|
|
U = 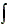 S * exp( - k * t) * dt = - S / k * exp( - k * t) + C. S * exp( - k * t) * dt = - S / k * exp( - k * t) + C. |
Подставляя последнее выражение в (9) получим:
|
|
P = (- S / k * exp( - k * t) + C) * exp(k * t) =
= C * exp(k * t) – S / k.
|
Полагая С = Ро и заменяя k на – (R + S) приходим к выражению (2).
Аналогично выводится соотношение
|
(11) |
Q = Qo * exp( - (S + R) * t ) + R / (S + R) |
при Qo > R / (S + R).
Поскольку в (2) имеется ограничение на величину Ро, дополним (в силу того, что P(t) = 1 – Q(t)) выражение (2) следующим образом:
|
(12) |
P = 1 - Qo * exp( - (S + R) * t ) - R / (S + R), |
что действительно при Po < S / (R + S), Qo = 1 – Po.
Таким образом, система уравнений (11,12) определяет поведение Э-триггера и представляет собой его аналитическую модель. Уравнения (1) определяют алгоритмическую модель Э-триггера.
Для оценки времени переходного процесса, обусловленного экспоненциальной природой поведения Э-триггера, воспользуемся известной в импульсной технике постоянной времени
Как принято считать, переходный процесс завершается в те-чение времени, равном 3Т = 3 / (R + S).
Достаточно легко убедиться в том, что при двоичных значениях (Po, R, S = 0, 1) Э-триггер ведет себя так же, как и обычный RS-триггер.
Экспоненциальная природа поведения Э-триггера представлена на примерах (рис. 2). Первый пример показан на рис. 2а. В исходном состоянии полагаем P = Q = 0.5, R = S = 0. Под воздействием единичного импульса R значение Р падает до нуля (Q как дополнение Р до единицы на рисунке не показывается). Затем через некоторое время появляется сигнал S = 0.1. После этого значение Р экспоненциально возрастает до единицы (при условии со-хранения значения S) за время, примерно равное 3/0.1t, что при t = 1 сек. составит 30 сек. (Отметим, что при исчезновении сигнала S до окончания указанного времени, значение Р станет постоянным и равным той точке экспоненты Р, которой соответствует исчезновение сигнала S.) Далее, согласно рис. 2а появляется сигнал R = S = 0.1. С этого момента значение Р уменьшается по экспоненте до величины 0.5 за время, примерно равное 3/(0.1+0.1)t. При принятом масштабе это время приблизительно равно 15 сек. Затем оба сигнала R и S одновременно исчезают, а значение Р сохраняется равным 0.5.
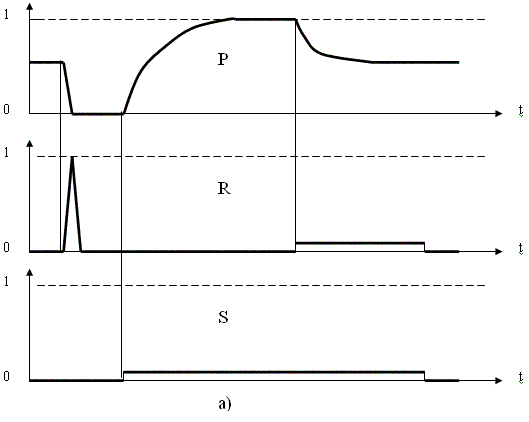
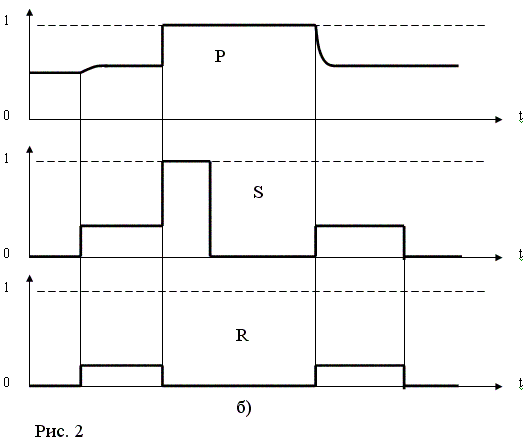
Изменение выхода Р рассматриваемого Э-триггера по экспоненте особенно ярко выражено при малых значениях сигнала S (R), так как при этом сравнительно большую величину имеет постоянная времени. Если имеет место только один из входных сигналов, то экспонента стремится к единице (при S > 0) или к нулю (при R > 0). Если длительность входного сигнала меньше трех постоянных времени, то запоминается последнее значение экспоненты на момент исчезновения входного сигнала.
Если на входы Э-триггера поступают одновременно два равных по величине сигнала (R = S), то экспонента стремится к значению Р = 0.5 (рис. 2а).
На рис. 2,б представлен пример поведения Э-триггера для случая неравных значений входных сигналов. В начале Р = 0.5, S = R = 0. При одновременном появлении сигналов S = 0.3 и R = 0.2 значение Р по экспоненте увеличивается до величины S / (S + R) = 0.6. Затем сигнал R сброса обнуляется, а сигнал S установки одновременно вырастает до единицы. При этом значение Р устанавливается в единицу. После этого переменная S обнуляется при сохранении установленной величины Р. Далее входные сигналы одновременно возникают в прежних значениях S = 0.3 и R = 0.2. Выходной сигнал Р по экспоненте уменьшается до той же величины
S / (S + R) = 0.6.
Из этого примера можно заключить, что, какое бы первоначальное значение не имела бы величина выходного сигнала Р, при различных, отличных от нуля, значениях входных сигналов, значение Р по экспоненте стремится к величине S / (S + R). Одновременно значение Q по экспоненте стремится к величине
R / (S + R). Таким образом, Э-триггер позволяет получить по окончании переходного процесса нормированное соотношение входных сигналов R и S.
Для более полного представления об Э-триггере приведенных примеров недостаточно, однако алгоритмическая (1) и аналитическая (11,12) модели позволяют воспроизвести любые ситуации с входными сигналами и начальными условиями Э-триггера.
Рассмотренный выше Э-триггер состоит из двух компонент-состояний, взаимно дополняющих друг друга до единицы.
В общем случае может иметь место многокомпонентный экспоненциальный автомат, каждая компонента которого подобна плечу Э-триггера, изменяет значение своего состояния в интервале [0,1], а сумма значений состояний всех компонент такого автомата тождественно равна единице.
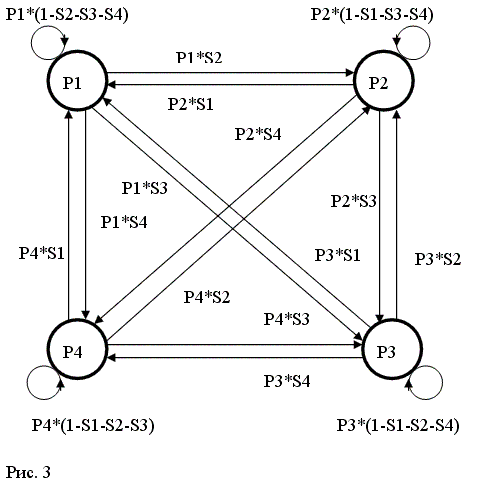
На рис. 3 изображен граф переходов четырехкомпонентного автомата, где имеют место следующие соотношения, определяемые общим правилом: значение Pi состояния i-го компонента возрастает при увеличении входного сигнала Si и убывает при увеличении любого из входных сигналов Sj (j не равно i):
|
(13) |
P1(t+1) = P1(t) * (1 – S2(t) – S3(t) – S4(t)) +
+ S1(t) * (P2(t) + P3(t) + P4(t)), |
|
|
P2(t+1) = P2(t) * (1 – S1(t) – S3(t) – S4(t)) +
+ S2(t) * (P1(t) + P3(t) + P4(t)), |
|
|
P3(t+1) = P3(t) * (1 – S2(t) – S1(t) – S4(t)) +
+ S3(t) * (P2(t) + P1(t) + P4(t)), |
|
|
P4(t+1) = P4(t) * (1 – S1(t) – S3(t) – S2(t)) +
+ S4(t) * (P1(t) + P3(t) + P2(t)), |
|
|
P1(t) + P2(t) + P3(t) + P4(t) = 1. |
В общем виде для N-компонентного автомата действительна следующая система:
|
(14) |
Pi(t+1) = Pi(t) * (1 - sum(Sj(t))) + Si(t) * sum(Pj(t)),
(j не равно i; i,j = 1,...,N),
P1(t) + ... + PN(t) = 1,
|
где sum обозначает арифметическую сумму.
Данные рекуррентные формулы напоминают рекуррентные формулы Э-триггера. Из этого можно предположить, что поведение компонент данного автомата также подчиняется экспоненциальному закону.
Подтвердим экспоненциальную природу N-компонентного автомата, удовлетворяющего приведенным соотношениям для N компонент-состояний:
|
(15а) |
Pi = Pi0 * exp(- K * t) – Si / K,
K = S1 + Е + SN,
i = 1,..,N:
при Pi0 > Si / K, |
|
(15б) |
Pi = 1 – sum(Pj),
Pj = Pj0 * exp(- K * t) – Sj / K,
j = 1,Е,N; j не равно i:
при Pi0 < Si / K. |
Заменим в (14) sum(Pj(t)):
|
(16) |
Pi(t+1) = Pi(t) * (1 – sum(Sj(t))) + Si(t) * (1 – Pi(t)) =
= Pi(t) * (1 – sum(Sk(t))) + Si(t),
k = 1,Е,N. |
Отсюда следует (по аналогии с доказательством для Э-триггера):
|
|
Pi(t+1) – Pi(t) = -Pi(t) * K + Si, где K = sum(Sk); |
|
(17) |
Pi' = - K * Pi + Si; |
При Si = 0 имеем K – Si = K, а так же по аналогии с доказа-тельством для Э-триггера получим
|
(18) |
Pi = Ui * exp(-K * t), |
где Pi0 – начальное значение Pi в момент времени t = 0.
При Si > 0 решение уравнения (17) будем искать в виде
|
|
Pi = Ui * exp(-K * t), где Ui = Ui(t). |
Дифференцируя по t получим
|
|
Pi’ = Ui’ * exp(-K * t) - Ui * K * exp(-K * t). |
Приравняем правую часть последнего выражения к правой части выражения (17), подставив в нее (18):
|
|
Ui' * exp(-K * t) - Ui * K * exp(-K * t) = -K * Ui * exp(-K * t) + Si |
Упрощая данное уравнение, получим
|
|
Ui' * exp(-K * t) = Si и, соответственно,
Ui' = Si * exp(K * t).
|
Интегрируя последнее выражение получим
|
|
Ui = 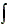 Si * exp(K * t) *dt = Si / K * exp(K * t) + Ci. Si * exp(K * t) *dt = Si / K * exp(K * t) + Ci.
|
Подставляя это выражение в (18) получим
|
|
Pi = (Si / K * exp(K * t) + Ci) * exp(-K * t) =
= Ci * exp(-K * t) + Si / K
|
Полагая Сi = Рi0, где Pi0 – начальное значение Pi в момент времени t = 0, приходим к соотношению (15).
Поведение Э-автомата, идентично поведению Э-триггера с той лишь разницей, что число входных и выходных переменных значительно больше.
В данной работе не представляется возможным изобразить многочисленные примеры поведения Э-автомата. Предложим лишь простейший пример.
Предполагаем, что исходным (неопределенным) значением состояния каждой из N компонент является величина Pi0 = 1 / N. При этом Si = 0 (для всех i = 1,…,N). Если на один из входов (например, на вход j (1 <= j <= N)) поступит сигнал Sj, незначительно превышающий ноль, а на остальные входы поступает ноль, то Pj по экспоненте устремится к единице, а остальные выходные сигналы по экспоненте (с той же постоянной времени) устремятся к нулю. Если через промежуток времени, исчисляемый примерно 3 / Sj , сигнал Sj постоянен, то значение выхода Pj установится равным единице, а значения остальных выходов станут равными нулю.
Таким образом, Э-автомат, в том числе и Э-триггер, позволяет посредством входного сигнала задавать временные задержки, а так же обеспечивать необходимый баланс выходных сигналов, в сумме дающих единицу. По окончании переходного процесса после произвольного скачкообразного изменения входного сигнала (сигналов) на j-м выходе устанавливается значение Sj / K. Это означает, что Э-автомат формирует нормированное соотношение входных сигналов. По сути - это модель гомеостата.
Помимо изложенного, следует отметить, что Э-автомат напоминает однослойную искусственную нейронную сеть, например сеть Хемминга или Хопфилда и обеспечивает нормализацию входных сигналов. Такая однослойная сеть (Э-автомат) может использоваться в нейронных сетях в качестве вспомогательного слоя.
Э-автоматы могут найти разнообразное применение. Приведем несколько примеров.
Если имеется несколько каналов связи, то посредством Э-автомата можно измерить соотношение уровня шумов. При этом, на входы Э-автомата подключаются выходы линий связи как генераторы сигналов шума при отсутствии полезного сигнала. Тогда диаграмма выходных сигналов Э-триггера покажет относительные уровни шумов в соответствующих каналах связи.
С помощью Э-автомата можно исследовать изменение во времени желаний, предпочтений или эмоциональных составляющих (и тому подобных подлежащих исследованию психо-физиологических компонент) индивидуума или определенной группы. Например, так можно проследить динамику формирования рейтинга кандидатов на выборную должность. При этом, на входы Э-автомата должны подаваться сигналы, соответствующие конкретным раздражителям, например, эмоциональный уровень агитационных доводов каждого из кандидатов. При этом такой сигнал может быть как кратковременным, так и долговременным, постоянного или переменного уровня. На выходе Э-автомата образуется динамика предпочтений индивидуума ко всем кандидатам.
Автор просит исследователей из различных областей науки попробовать поэкспериментировать с Э-автоматами, в том числе в среде MATLAB. За консультацией и с возможными результатами обращаться по E-mail : bpk@rednet.ru
Если кто-то захочет открыть форум или новостную рассылку, просьба известить автора.
Иллюстрации: примеры работы Э-автоматов
(BORLAND C++ BUILDER)
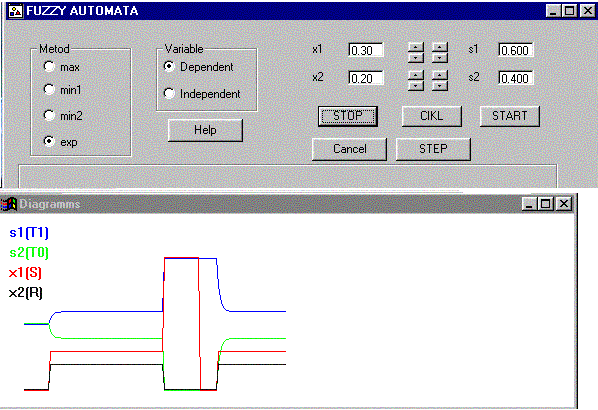
рис 4.
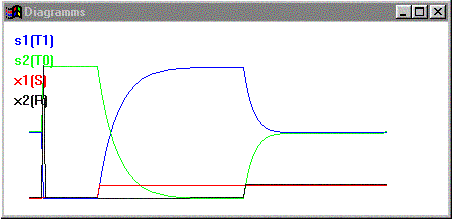
рис 5.
|