Последовательно-событийные автоматы

Отсюда можно скачать полный текст статьи в формате html (87 кб)

УДК 62-507

© Б.П. Кузнецов

boris@actor.ru

Федеральный научно-производственный центр ГУП "НПО "Аврора""

Печатная версия опубликована в журнале "Приборы и системы.Управление, контроль, диагностика", 2001 N 5

Рассматриваются программно реализуемые конечные автоматы с последовательным вычислением событий, обуславливающих переходы.

Содержание

1. Введение
2. Последовательное вычисление событий
3. Выходы автомата
4. Состояния автоматов
5. Структура последовательно-событийного автомата
6. Задание бесповторного автомата
7. Автоматы со скрытыми переходами и состояниями
8. Автоматы с обобщенными состояниями
9. Декомпозиция состояний - многополюсников
10. Заключение
11. СПИСОК ЛИТЕРАТУРЫ

1. Введение

Конечные автоматы Мура и Мили предложено использовать в программах общего назначения (не только для логического управления) сравнительно давно [1]. При этом наиболее разработанным вопросом применения конечных автоматов является синтаксический анализ в различного рода трансляторах алгоритмических языков [2]. В настоящее время интерес к использованию конечных автоматов в программировании возобновляется, например, в области логического управления [3] и в объектно-ориентированном программировании [4].

В известных применениях процесс вычисления входной информации автоматов вынесен за пределы соответствующей, реализующей автомат, подпрограммы, например [3]. Поэтому такие автоматы можно реализовать не только с помощью программы, но и на элементах параллельной логики по одному и тому же классическому заданию. Такие программно реализуемые автоматы будем называть автоматами с независимыми событиями (АНС).

По опыту автора, конечные автоматы можно применять для описания алгоритмов произвольных циклических программ разнообразного назначения, а также подпрограмм, включающих запоминаемые от вызова подпрограммы до следующего ее вызова некоторые данные [5]. Однако известные модели конечных автоматов не учитывают некоторых особенностей их программной реализации в указанных случаях, в частности, именно последовательного способа реализации вычислений и использования механизма циклов. В данной работе предлагается новая модификация модели программно реализуемых автоматов для обеспечения универсальности их применения.

2. Последовательное вычисление событий

Говоря о программной реализации автоматов будем иногда ссылаться на языковые особенности, подразумевая наиболее распространенный универсальный язык программирования С++ [6].

Состояния автоматов как на графе переходов, так и в таблицах (массивах) переходов и выходов или в операторах множественного выбора будем обозначать либо буквами латинского (русского) алфавита либо произвольными целыми числами (не обязательно следующими подряд).

Для вычисления букв входного алфавита автомата будем использовать логические выражения, которые могут содержать наряду с булевыми переменными и операциями так же и операции сравнения как целочисленных так и вещественных переменных, в том числе типовых и оригинальных целочисленных и вещественных функций с произвольными параметрами. Так же в качестве целочисленных переменных могут быть использованы и адресные переменные, в том числе указатели на объекты классов.

Приведем примеры логических выражений (которые будем записывать в круглых скобках):

• (a | b & с) – выражение с булевыми переменными (примитивная булева формула;
• (А >= 0.15 & B < А) – использование сравнения и логического И;
• (exp(X) != sin(Y)) – сравнение вещественных функций;
• (n--) – не нулевое значение целого числа с декрементом;
• (a & func1(A,B)) – логическое И булевой переменной и ненулевого значения целочисленной функции с двумя параметрами;
• (Тxt & len(Txt)) – наличие объекта текстового класса ненулевой длины.

Логическое выражение будем обозначать Xk = (…), где k – порядковый номер выражения. Другим обозначением логического выражения будем использовать конструкцию вида Xa_n, Xb_n и так далее, где a (b) – обозначения состояний, n – порядковый номер дуги, исходящей из вершины a (b).

Событием Ti_n будем называть выражение вида

1. Ti_n = ~Ti_n-1 & [Аi_n -> Xi_n],

Ti_1 = [Ai_1 -> Xi_1],

где i – обозначение состояния, Ai_n – обозначение подпрограммы, которую будем называть активизирующим действием, предназначенным для вычисления, или подготовки к вычислению, одного или нескольких аргументов логического выражения Xi_n; стрелка “->” означает: сначала выполнить действие слева от нее, а затем вычислить значение (ноль, не ноль) логического выражения, стоящего справа от стрелки; в целом значение выражения, заключенного в квадратные скобки, равно нулю при нулевом значении логического выражения Xi_n, и равно единице в противном случае [7] (напомним, что логическое выражение, не равное нулю, может принимать произвольное целочисленное, в том числе отрицательное, значение).

Программно реализуемый автомат с буквами входного алфавита вида (1) будем называть последовательно-событийным автоматом (ПСА) ввиду того, что вычислению очередного события предшествуют не только последовательное вычисление нескольких логических выражений, но и последовательное вычисление активизирующих действий.

Дуги (петли) переходов ПСА помечаются обозначением событий или правой частью выражений (1). Как следует из (1), события ранжированы во времени их вычисления, начиная с простейшего события вида Ti_1 = [Ai_1 -> Xi_1].

Если логические выражения и активизирующие действия не повторяются в определениях всех событий, то ПСА будем считать бесповторным (БПСА).

Другим обозначением событий в БПСА будем считать двухиндексное, вида Tij, где i – номер вершины графа переходов (состояния или обозначающая его буква), из которого исходит дуга, помеченная данным событием, а j – номер вершины, в которую заходит эта дуга. Например, событие на переходе из вершины a в вершину b обозначается Tab.

С учетом бесповторности событий будет иметь место и одноиндексное обозначения вида Tj, где j – порядковый номер события, не превышающий общего числа событий в БПСА.

3. Выходы автомата

Вместо булевых переменных, образующих выходной алфавит АНС логического управления, в БПСА указываются подпрограммы (операторы). Приведем примеры выходов БПСА, являющихся подпрограммами, то есть действиями, заключенными в фигурные скобки:

• {А++; B = 4.23;} – последовательность операций единичного приращения переменной и операции присваивания;
• {С = ln(x);} – вычисление логарифма и присваивание;
• {F = fopen(…); } – открытие файла;
• { Tv = new Tver; } – инициализация объекта класса Tver;
• {func1(x); func2(y); Z=func3(A-B,tg(c));} – последовательность произвольных подпрограмм и операторов, в том числе в качестве подпрограмм могут быть использованы вложенные ПСА.

Вместо единственного выходного алфавита в ПСА могут иметь место три выходных алфавита.

Рассмотрим рис.1, где изображена вершина графа переходов БПСА и несколько исходящих из нее дуг переходов и петля.

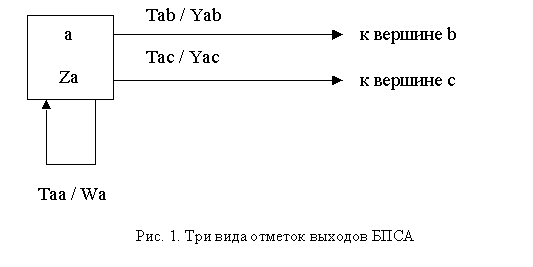
Вершина указана прямоугольником, внутри которого в верхней части показывается обозначение состояния, в данном случае “a”; в нижней части показывается обозначение подпрограммы, всегда выполняющейся в данном состоянии и которую будем называть подпрограммой – телом состояния. В общем случае тело состояния необходимо для определения переменных, используемых при вычислении событий. (В [3] все переменные, входящие в булевы формулы на дугах графов переходов, определяются вне программы, реализующей автомат.) Кроме того, в теле состояния могут инициализироваться и завершаться операции типа открытия-закрытия файлов, ввода-вывода записей файлов, определения-уничтожения объектов классов, реализации вложенных ПСА и так далее. Тело состояния будем обозначать символом Zi, где i – обозначение состояния. Тело состояния соответствует выходу автомата Мура. Множество обозначений тел состояний образует первый выходной алфавит Z = {Z1,…,ZN}, где N – число состояний БПСА, например: Z = {Za, Zb, Zc, Zd}.

Подпрограммы-выходы, указываемые на дугах переходов к другим вершинам, в данном случае на дугах ab и ac, будем обозначать символом Yij, где i и j – обозначения состояний “откуда – куда”, соответственно. Эти подпрограммы также будем считать бесповторными, что дает возможность обозначать их символом Yk, где k – порядковый номер дуги перехода (исключая петли) в БПСА. Такие подпрограммы соответствуют выходам автомата Мили и образуют второе множество выходов Y = {Y1,…YL}, где L – число дуг переходов БПСА, исключая петли.

Третьим типом выходов БПСА будем считать подпрограммы, указанные на петлях и обозначаемые Wi, где i – обозначение состояния (рис. 1). Такие отметки (подпрограммы) образуют третий выходной алфавит W = {W1,…,WN}, где N – число петель (состояний БПСА).

4. Состояния автоматов

Состояния образуют алфавит S = {S1,…,SN}, где S1 = ‘a’, S2 = ‘b’,…, например: S = {a, b, c, d}. Начальное состояние S1. Назначение тела состояния Zi заключается в следующем: во-первых, последовательно сформировать текущие значения аргументов логических выражений, и, во-вторых, инициировать необходимое очередное событие.

Рассмотрим подробнее тело Zi i-го состояния ПСА, изображенного на рис. 2.

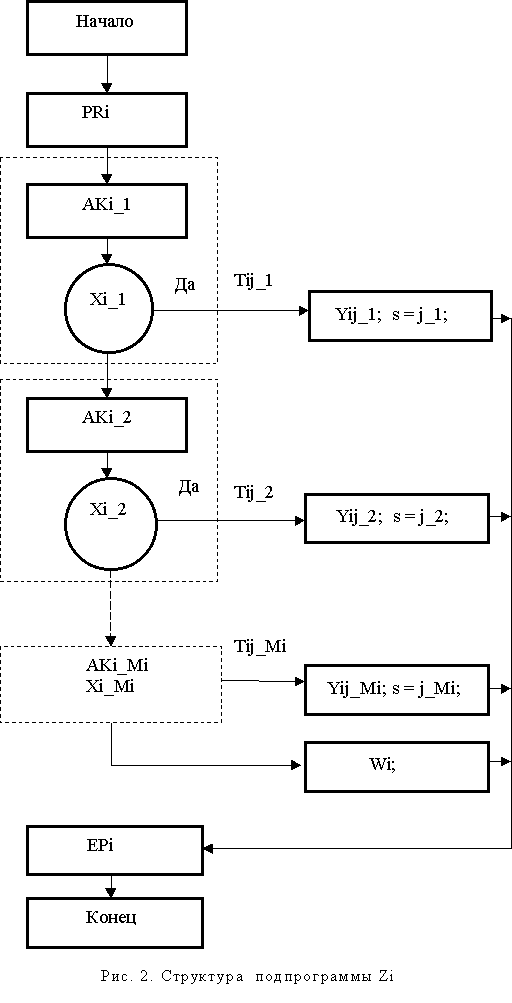
Подпрограмма Zi начинается выполнением ряда инициирующих действий, общих для всех активизирующих действий и логических выражений, используемых для определения очередного перехода в другое состояние. Эти действия заключены в подпрограмме PRi. Последнюю будем называть прологом тела состояния, в котором выполняются, например, такие действия как открытие или чтение записи файла, ввод данных с периферийных устройств, реализация функций объекта класса, вызов вложенного ПСА и прочие инициализирующие операции.

Далее следует последовательность подпрограмм, которые на рис. 2 выделены пунктиром и которые будем называть бинарными трехполюсниками. Каждый бинарный трехполюсник состоит из необязательной активизирующей подпрограммы (AKi_1, AKi_2,…,AKi_Mi, где Mi – число бинарных трехполюсников в теле i-го состояния ПСА, или число событий, инициируемых в i-ом состоянии) и проверки истинности логического выражения (Xi_1, Xi_2,…,Xi_Mi). Активизирующая подпрограмма подготавливает необходимые данные для проверки логического выражения. Бинарный трехполюсник (n-й по порядку) имеет один вход и два выхода: первый выход означает истинность логического выражения и соответствует инициации события Ti_n, второй выход соответствует невыполнению логического условия Xi_n и связан со входом следующего по порядку бинарного трехполюсника. (Второй выход последнего бинарного трехполюсника рассмотрим далее.)

Совокупность бинарных трехполюсников образует бинарный многополюсник. Последний вкупе с прологом и эпилогом и составляет тело Zi состояния i.

Перейдем к рассмотрению действий, показанных на рис. 2 справа от бинарных трехполюсников. Пусть, например, в результате проверки логического условия Xi_1 инициировано событие Tij_1, в результате чего ПСА должен перейти в состояние j_1 c одновременной реализацией подпрограммы (выхода) Yij_1. Для реализации этого выполняется следующая подпрограмма: вызывается подпрограмма Yij_1, затем выполняется присваивание s = = j_1, где s – переменная, в которой запоминается текущее состояние ПСА. Указанные в прямоугольниках (в правой части рис. 2) действия выполняются для каждого события, соответственно инициированного бинарными трехполюсниками.

Второй выход последнего (Mi-го) бинарного трехполюсника соответствует случаю, когда ни одно из событий Tij не инициировано. Этот выход связан с реализацией подпрограммы Wi, выполняющейся на петле у i-й вершины.

Бинарные трехполюсники, показанные на рис. 2, будем называть активными. Если в бинарном трехполюснике отсутствует активизирующая подпрограмма (AKi_n), то такой трехполюсник будем называть пассивным. В последнем предполагается, что все данные для вычисления значения соответствующего логического условия получены в подпрограмме – прологе (PRi) или вне подпрограммы ПСА.

Завершает подпрограмму Zi подпрограмма-эпилог EPi, в которой выполняются операции по завершению функционирования действий, реализованных в подпрограмме-прологе, например, закрываются файлы, удаляются объекты классов и прочие.

5. Структура последовательно-событийного автомата

Перейдем к рассмотрению блок-схемы программной реализации подпрограммы ПСА в целом (рис. 3). Подпрограмма ПСА начинается выполнением пролога PRA, в котором открываются файлы, вводится информация с периферийных устройств, создаются новые объекты классов и реализуются другие действия, которые позволят выполнить прологи тел всех состояний, активизирующие действия и проверять логические выражения. Соответственно подпрограмма ПСА завершается эпилогом EPA, в котором отменяются инициирующие действия пролога.

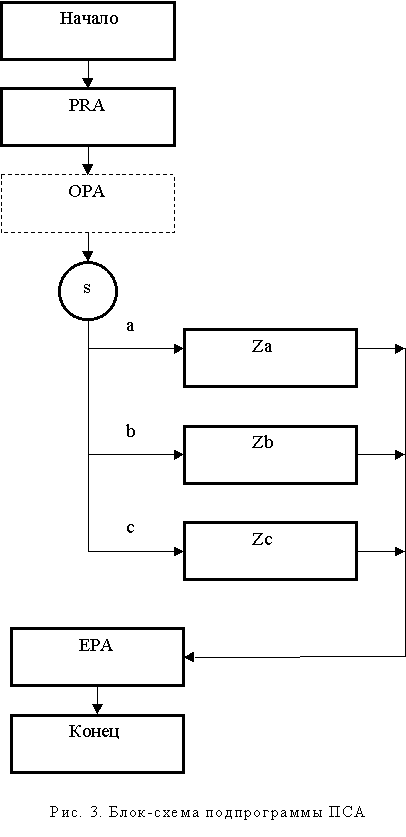
В подпрограммах ПСА, не являющимися БПСА, может присутствовать подпрограмма общих переходов (ОРА) из так называемых обобщенных состояний (см. ниже).

Основным компонентом подпрограммы ПСА является конструкция множественного выбора, в которой в зависимости от текущего значения переменной состояния s (a, b, c) выполняется соответствующая (рассмотренная ранее) подпрограмма – тело состояния (Za, Zb, Zc).

Начальное значение переменной состояния присваивается при первой инициализации подпрограммы ПСА.

6. Задание бесповторного автомата

Определим БПСА в стиле, близком к классическому, например [8]. Если БПСА задать в виде {T, S, Z, W, Y, …}, где T – входной алфавит, S – множество состояний, Z – первый выходной алфавит, и так далее, то представляет большое затруднение задать структуру элементов множества Z (прологи, эпилоги, активизирующие действия и прочее). Поэтому исключим Z из описания автомата за счет введения дополнительных множеств.

БПСА назовем систему

C = { S, T, Y, W, A, X, P, E, r, u, v, f },

где S = {S1,…,SN} – множество состояний, N – число состояний, Т = {T1,…,TL} – множество событий, L – число бесповторных событий, Y = {Y1,…,YL} – множество действий, реализуемых по соответствующим событиям, W = {W1,…,WN} – множество действий, реализуемых при отсутствии событий, инициируемых соответствующими состояниями, A = {A1,…,AL} – множество активизирующих действий для соответствующих событий, X = {X1,…,XL} – множество логических условий, отвечающих соответствующим событиям, P = {P0,P1,…,PN} – множество прологов: P0 – БПСА в целом, P1 – PN – состояний, E = {E0,E1,…,EN} – множество эпилогов (нумерация элементов аналогична P), r = {r1,…,rN} – множество старших индексов событий (см. ниже), u: S*T -> S – функция переходов, v: S*T -> Y – функция выходов, f = {f1,…,fL} – множество двоичных признаков скрытых переходов (см. ниже, раздел 7).

Каждому состоянию БПСА соответствуют инициируемые в его теле события, причем ни одно событие не инициируется более чем одним состоянием. Считаем, что события с номерами 1 – r1 инициируются состоянием S1, события с номерами r1+1 – r2 – состоянием S2, и так далее. Таким образом, элементы множества r обозначают старший номер события, инициируемого соответствующим состоянием. Отсюда следует

T_j = ~T_j-1 & [A_j -> X_j] при j-1 П r,

T_j = [A_j -> X_j] при j = 1, или j-1 О r.

В отличие от АНС задать БПСА традиционной автоматной таблицей (таблицей переходов и выходов) не представляется возможным из-за обилия взаимосвязанных компонент. Поэтому для описания БПСА предлагается использовать список событий, элемент которого соответствует одному переходу и имеет вид

<s1, p, g, x, t, f, y, s2, w, e >,

где s1,s2 О S, p О P, g О A, x О X, t О T, y О Y, w О W, e О E.

Для наглядности можно использовать и граф переходов, в котором условием на дугах указаны события без способа их получения.

Рассмотрим пример задания БПСА с четырьмя состояниями. Граф переходов БПСА изображен на рис. 4.

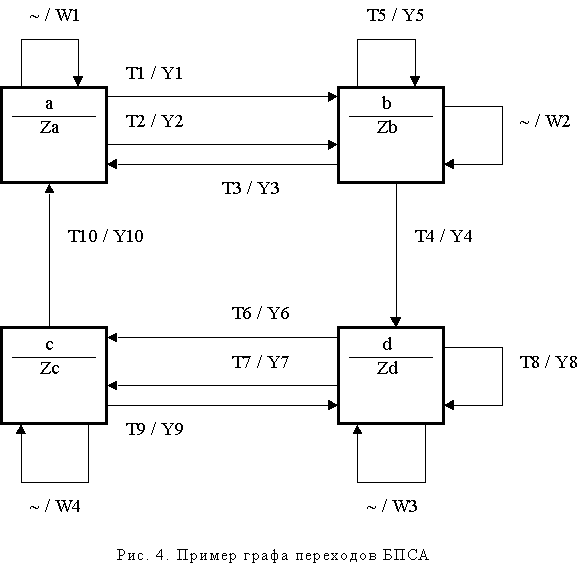
В состояниях a, b, c, d реализуются бинарные многополюсники, соответственно Za, Zb, Zc, Zd, формирующие события T1 – T10. Каждое событие Tj инициирует соответствующую подпрограмму Yj (j = 1,…,10). Если ни одно из событий, формируемых многополюсником какой либо вершины, не случилось, то реализуется соответствующая подпрограмма Wa (Wb, Wc, Wd).

Из рисунка следует, что из-за наличия нескольких дуг, исходящих из вершины a (d) и заходящих в одну и ту же вершину b (c), а также наличия двойных петель у вершин b и d, граф переходов является мультиграфом, что характерно для ПСА в отличие от АНС.

Граф на рис. 4 не раскрывает сути бинарных многополюсников, не показывает пролога и эпилога программы ПСА в целом. Поэтому вводится дополняющий граф переходов таблица-список событий (табл. 1). В этом списке, конкретизируется структура бинарного многополюсника, представленного на рис. 2, применительно к каждому из состояний БПСА, изображенного на рис. 4. Указанный список требует следующих пояснений.

Таблица 1.

Список событий ( дополнение к рис. 4 )

В графе “s1” указывается текущее состояние БПСА. В графах “p” и “e” задаются действия прологи и эпилоги, соответственно. При этом выделяется отдельная строка (первая) таблицы-списка для указания пролога P0 и эпилога E0, общих для БПСА в целом.

В графе “g” показаны активизирующие действия из многополюсника, причем для части из них указаны условия реализации в виде отрицания события, которое не наступило при проверке истинности логического выражения, указанного в предшествующей строке. Например, выражение ~T1/A2 обозначает: если событие T1 не наступило, то выполнить подпрограмму А2 и далее проверить истинность логического выражения X2 из соседней справа графы той же строки списка. Таким образом, каждое событие возможно только при невыполнении предыдущего события.

Состояния (“s2”) переходов и действия (“y”) на дугах (кроме действий (“w”) на петле) из-за ограниченности формата страницы в табл. 1 не представлены.

Действие (“w”) на петле, например, W1 реализуется только в том случае, если ни одно из указанных для состояния “a” событие не произошло. (На рис. 4 указаны и такие петли, которые реализуют оговоренные события, например, Т5 и Т8.)

Конечно, возможно обойтись и без списка событий, если в БПСА нет прологов и эпилогов. При этом следовало бы вводить специальные отметки на дугах переходов, например, вида

[ T2 = [ ~T1 / A2 -> X2 ]] / Y2,

смысл которой несложно раскрыть, используя рис. 4 и табл. 1.

Таким образом, основное отличие БПСА от АНС состоит в наличии активизирующих действий и механизма отрицания событий, а также прологов и эпилогов, что требует табличного способа задания БПСА при необязательном задании графа переходов.

7. Автоматы со скрытыми переходами и состояниями

Рассмотренные БПСА и АНС как подпрограммы реализуют только один переход, после чего передают управление программе более высокого уровня и повторно вызываются для реализации следующего перехода. Поэтому временной интервал между соседними переходами исчисляется не только временем реализации автомата, но и временем работы вызывающей программы.

В ряде случаев необходимо продолжить выполнение переходов не выходя из тела подпрограммы БПСА. Такая ситуация возникает при необходимости соблюдения определенного быстродействия подпрограммы БПСА или при необходимости продолжать вычисления с не возобновляемыми данными. Для реализации таких случаев предлагается механизм скрытых переходов и скрытых состояний.

Суть данного механизма состоит в том, что некоторый переход приводит не к завершению подпрограммы БПСА, а к возврату в ее начало. При этом может быть заблокировано выполнение прологов и эпилогов. Для реализации такого процесса в БПСА вводится флаг скрытого перехода (ФСП). При наступлении некоторых заданных событий ФСП принимает единичное значение, а при наступлении остальных событий ФСП обнуляется. Перед завершением подпрограммы БПСА проверяется ФСП, и, если он не нулевой, то выполняется возврат к началу подпрограммы БПСА. Другими словами подпрограмма БПСА, содержащая ФСП, имеет собственный цикл.

Если БПСА повторно реализуется в собственном цикле, то его переменная – состояние на все время пребывания в цикле недоступна другим программам. Поэтому переходы, соответствующие установке ФСП (в единицу) называются скрытыми. Если все переходы в некоторое состояние, в том числе петли, приводят к установке ФСП, то такое состояние называется скрытым, так как никакой другой программе данное состояние недоступно.

Для блокировки прологов и эпилогов используется простая конструкция выбора “ЕСЛИ ФСП = 0 ТО Pi (Ei)”.

Скрытые переходы на графе переходов обозначаются перечеркиванием соответствующей дуги [9]. Так, например, граф переходов, изображенный на рис. 5 содержит скрытые переходы по событиям Т1, Т2, Т3, Т5, а также скрытую петлю у вершины b.

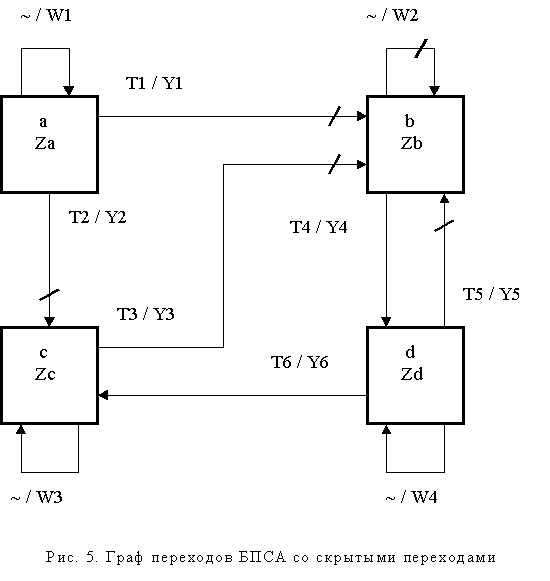
Этот граф содержит скрытое состояние b. В граф-схемах явно указывается установка, сброс и проверка ФСП. На рис. 6, 7 показаны соответствующие фрагменты БПСА, реализующего граф переходов (рис. 5). В списках событий ФСП упоминается в графах “p”, “t”, “e”. В таблице 2, задающей события для БПСА по рис. 5, символом F обозначен ФСП.

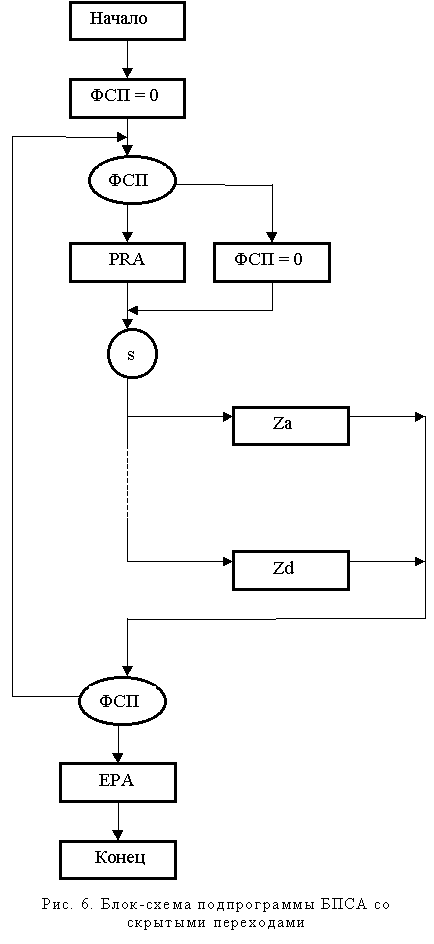
Как следует из рис. 6, сокрытие переходов и состояний обеспечивается собственным циклом подпрограммы БПСА, обеспечиваемым не нулевым значением ФСП, устанавливаемым в блоках реализации состояний и событий, например, согласно рис. 7. Подпрограмма возвращает управление вызвавшей ее программе только в том случае, когда ФСП установлен в ноль.

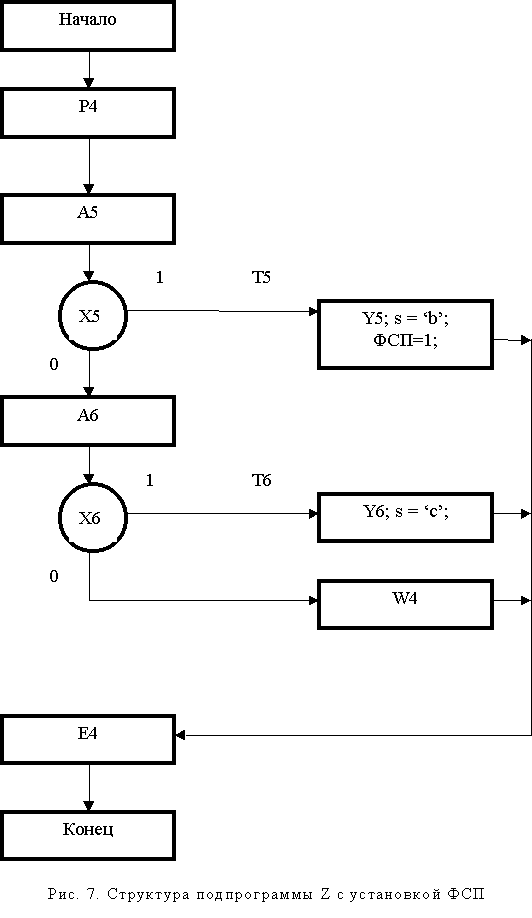
Таблица 2.

Список событий и ФСП ( дополнение к рис. 5 )

Установка и проверка ФСП могут отличаться от приведенного примера, но основная цель – сокрытие переходов в цикле должна быть достигнута. БПСА может содержать более одного ФСП, например, скрытое состояние может иметь собственный ФСП для блокирования в цикле его пролога и эпилога и даже активизирующих действий.

8. Автоматы с обобщенными состояниями

Граф переходов ПСА может содержать дуги, помеченные одинаковыми парами “событие / действие” и направленные в одну и ту же вершину. Такой автомат не является БПСА, но при определенных условиях может быть преобразован в последний.

Рассмотрим такой ПСА, граф переходов которого изображен на рис. 8а (для упрощения рисунка петли у вершин не показаны). Дуги ab, cb, db направлены в вершину b и имеют одинаковые пометки “T1 / Y1”. Налицо явный повтор переходов. При выполнении указанных позже условий можно преобразовать данный повторный автомат в бесповторный. Для реализации такого преобразования введем в граф переходов дополнительную вершину, так называемого обобщенного состояния. Последнее обозначается списком идентификаторов вершин, из которых исходят упомянутые, одинаково помеченные и направленные, дуги. В нашем примере на рис. 8б представлена (штриховым контуром) вершина обобщенного состояния, помеченная списком “a, c, d”. Из этой вершины исходит дуга, направленная в вершину b и помеченная парой “T1 / Y1”. Дуги, помеченные аналогично на рис. 8а, исключены в новом графе переходов. Полученный таким образом автомат является бесповторным, так как не содержит одинаково помеченных дуг на графе переходов.

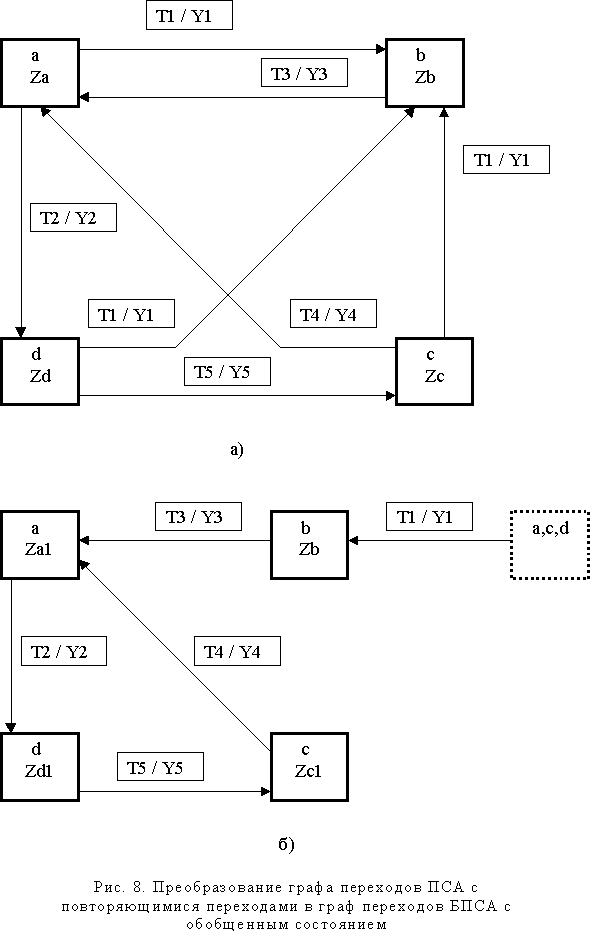
Такой БПСА реализуется следующим образом. После исполнения пролога проверяется текущее состояние БПСА, и, если оно входит в список, отмечающий обобщенное состояние, то реализуется попытка получения события T1. При наличии T1 выполняется подпрограмма Y1 и осуществляется переход в состояние b, после чего реализуется эпилог и выход из подпрограммы БПСА до следующего глобального цикла. При отсутствии события T1 реализуется соответствующий переход из штатных вершин.

Таблица – список событий БПСА с обобщенным состоянием в качестве первой строки после строки пролога содержит в графе “текущее состояние” список идентификаторов, отмечающих обобщенное состояние и соответствующую информацию по формированию события T1 в остальных графах. Список событий и блок-схемы реализации БПСА с обобщенным состоянием не приводятся в целях экономии объема статьи.

Перейдем к рассмотрению условий получения обобщенного состояния. Помимо описанного (первого) условия наличия одинаково помеченных и направленных переходов существует еще два условия.

Второе условие состоит в том, что прологи тел состояний, из которых осуществляется указанный переход, должны быть одинаковыми, в том числе пустыми (отсутствующими), или трехполюсник, реализующее повторяющееся событие, не зависит от прологов указанных состояний.

Третье условие предполагает, что трехполюсники, реализующие одинаковые повторяющиеся события, должны быть первыми в соответствующих состояниям (с указанным событием) многополюсниках, или могут быть переставлены на первое место. Рассмотрим последнее утверждение.

В [5] дано понятие о независимых и зависимых фрагментах – двухполюсниках. Аналогичное понятие введем и для трехполюсников, входящих в подпрограммы-многополюсники Zi.

Допустим в многополюснике Zi имеются два трехполюсника, описываемых выражениями

“T1 = [A1 -> X1]” и “T2 = ~T1 & [ A2 -> X2]”.

Если допустимо их преобразование к виду

“T2 = [A2 -> X2]” и “T1 = ~T2 & [A1 -> X1]”,

то есть выполняется перестановка трехполюсников без потери сущности событий T1 и T2, то такие трехполюсники будем называть независимыми. Если перестановка трехполюсников в указанном смысле недопустима, то такие трехполюсники будем называть зависимыми.

Следовательно, конкретный трехполюсник может быть переставлен на первое в многополюснике место, если он и выше расположенные трехполюсники независимы.

В общем случае, число обобщенных состояний может быть два и более, но в данной статье этот вопрос обсуждаться не будет.

9. Декомпозиция состояний - многополюсников

Представленные графы переходов БПСА воспринимаются сложнее, чем традиционные АНС, хотя список событий читается сравнительно легко. С целью приведения БПСА к виду, напоминающему традиционный самодостаточный граф переходов АНС, выполняется декомпозиция состояний на основе вычленения отдельных трехполюсников из многополюсников. Покажем на примере как это делается.

Возьмем граф переходов БПСА, изображенный на рис. 4, и дополняющую его табл. 1. Составим на их базе новый граф переходов с числом вершин, равным числу вершин исходного графа плюс число событий. Вершины расположим в 4 горизонтальных ряда, соответствующих состояниям рассматриваемого БПСА.

Каждый ряд включает начальную вершину, реализующую пролог состояния, и вершины, реализующие события, инициируемые в указанном состоянии. В частности первый ряд (рис. 9) соответствует состоянию “a” исходного графа переходов и включает вершины: “a0” – вершина, реализующая пролог P1, “a1” – вершина, реализующая действие А1 и инициирующая событие T1, “a2” – вершина, реализующая действие А2 и инициирующая событие T2. Из вершины “a0” в вершину “a1” направлена непомеченная условием и действием дуга скрытого перехода. Из вершины “a1” в вершину “b0” (состояние “b” исходного БПСА) направлена дуга , помеченная условием X1 и действием Y1 (реализация события T1). Из той же вершины “a1” в вершину “a2” направлена дуга скрытого перехода, помеченная условием ~X1 (не состоявшееся событие T1). Из вершины “a2” в вершину “b0” направлена дуга, соответствующая реализации события T2, а в вершину “a0” направлена дуга, реализующая петлю “~T2 / W1” исходного графа переходов. Аналогично строятся остальные вершины и дуги нового графа переходов БПСА.

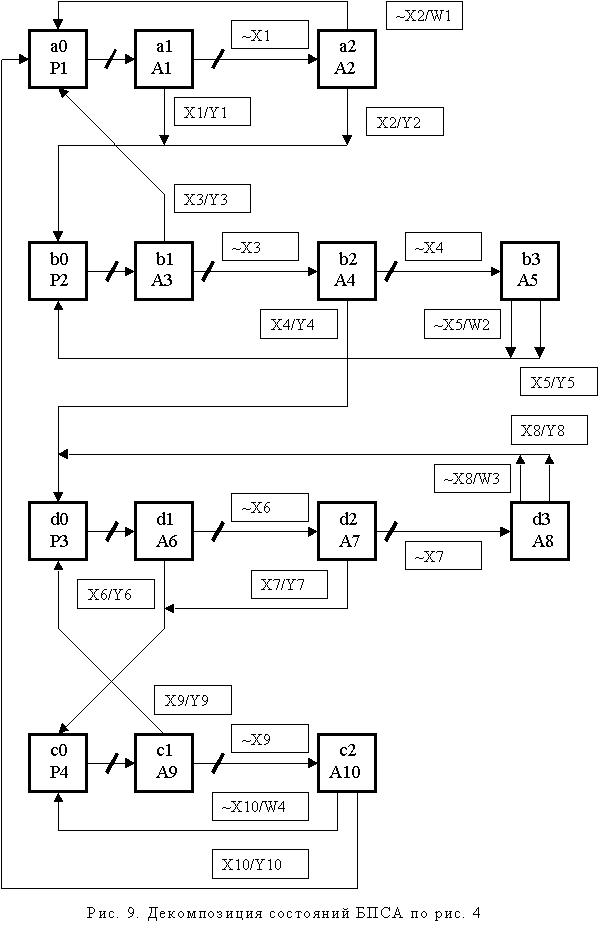
От графа переходов АНС полученный на рис. 9 граф отличается отсутствием петель и наличием скрытых переходов. Этот граф напоминает Р-схему [10], но отличается от последней наличием скрытых переходов.

Состояния полученного графа будем называть “субсостояниями” БПСА. Субсостояния, связанные скрытыми переходами, вкупе соответствуют состоянию исходного графа переходов.

Отметим так же, что на рис. 9 не указаны пролог P0 и эпилоги из-за ограниченности места. На самом деле в состояниях “a0”, “b0”, “c0”, “d0” перед обозначением пролога состояния должно присутствовать обозначение пролога БПСА P0. Каждая дуга, не являющаяся скрытым переходом, должна быть помечена дополнительно действиями – эпилогами состояния и БПСА. Например, вместо указанной на рис. 9 пометки “X1 / Y1” следует написать пометку “X1 / Y1, E1, E0”.

Таким образом исходный БПСА декомпозируется в граф переходов с субсостояниями и скрытыми переходами, не требующий дополнения в виде списка событий.

Имеет место обратная задача – получить по такому графу список событий, которую здесь не рассматриваем.

10. Заключение

Представленные БПСА имеют следующие отличия от известных автоматов.

1. В АНС аргументы логических условий получают вне подпрограммы-автомата, а в БПСА – внутри подпрограмм-многополюсников (в субсостояниях).
2. В АНС имеют место только пассивные независимые трехполюсники, в то время как в БПСА – активные зависимые трехполюсники
3. В АНС отсутствуют прологи и эпилоги состояний, а в БПСА они имеют место.
4. Только в БПСА наличествуют скрытые переходы и имеется собственный цикл.
5. АНС могут быть однозначно реализованы аппаратно, в то время как БПСА реализуются только программым путем.

В целом БПСА предоставляют больше возможностей для реализации подпрограмм широкого профиля (не только логического управления).

СПИСОК ЛИТЕРАТУРЫ

1. Байцер Б. Архитектура вычислительных комплексов. Том I. – М.: Мир, 1974.
2. Ахо А., Ульман Дж. Теория синтаксического анализа, перевода и компиляции. Том 1. Синтаксический анализ. - М.: Мир, 1978.
3. Шалыто А.А. SWITCH-технология. Алгоритмизация и программирование задач логического управления. – СПб.: Наука, 1998.
4. Гради Буч. Объектно-ориентированный анализ и проектирование с примерами приложений на С++. – М.: “Издательство Бином”, СПб: “Невский диалект”. 1998.
5. Кузнецов Б.П. Структура и сложность модулей циклических программ. // А и Т № 2, 1999. С. 151 – 165.
6. Киммел П. Borland C++ 5. СПб.: BHV – Санкт-Петербург, 1997.
7. Грэхем Р., Кнут Д., Поташник О. Конкретная математика. Основание информатики. М.: Мир, 1998.
8. Баранов С.И. Синтез микропрограммных автоматов. Л.: Энергия, 1979.
9. Кузнецов Б.П. Стандартная реализация управляющих программ // Судостроительная промышленность. Сер. Системы автоматизированного проектирования. 1986. № 1. C. 51 – 55.
10. Вельбицкий И.В., Ходаковский В.Н., Шолмов Л.И. Технологический комплекс производства программ на машинах ЕС ЭВМ и БЭСМ-6. – М.: Статистика, 1980.