Распределенные конечные автоматы

Отсюда можно скачать полный текст статьи в формате html (47 кб)

УДК 681.3.06

© Б.П. Кузнецов

boris@actor.ru

Федеральный научно-производственный центр ГУП "НПО "Аврора""

Печатная версия опубликована в журнале "Приборы и системы. Управление, контроль, диагностика", 2000 N 2.

Рассматривается алгоритм управления, заданный моделью конечного автомата, распределенный по процессорам многопроцессорной системы. Предложен способ декомпозиции таких автоматов.

1. Введение

Технологические процессы управления могут быть распределены в пространстве [1] (например, технологические линии, технические средства судов, нефте-(газо-)проводы) и требуют для их автоматизации многопроцессорной системы.

Алгоритм управления таким распределенным технологическим процессом может быть задан графом переходов конечного автомата с последующей его декомпозицией (распределением по процессорам). В процессе декомпозиции вместо одного графа переходов с заданным множеством состояний появляется набор графов переходов, каждый из которых имеет свое множество состояний, отличное от исходного [2].

В настоящей работе предложен упрощенный способ декомпозиции конечного автомата - составления и разбиения алгоритма по процессорам многопроцессорной системы управления распределенными технологическими процессами в едином пространстве состояний.

2. Простейшие распределенные автоматы Мура

Представим себе следующий процесс. Имеется контроллер для автоматического управления некоторым технологическим процессом и операторская станция со своим процессором для визуального наблюдения за этим процессом. Алгоритм управления задан графом переходов (рис. 1А) управляющего автомата, реализуемого контроллером. В прямоугольнике, обозначающем вершину, в верхней части указан идентификатор состояния (“А”, “B”, “C”), а в нижней части указан идентификатор действия (Ya,Yb, Yc), то есть управляющее воздействие, выполняемого автоматом Мура в данном состоянии. Дуги, связывающие вершины, отмечены условием соответствующего перехода (например, дуга из вершины A в вершину B отмечена условием перехода Xab, и так далее). Петли, сохраняющие текущее состояние автомата на рисунке не показаны, но подразумеваются, причем пометка петли содержит отрицание дизъюнкции условий переходов из данного состояния.

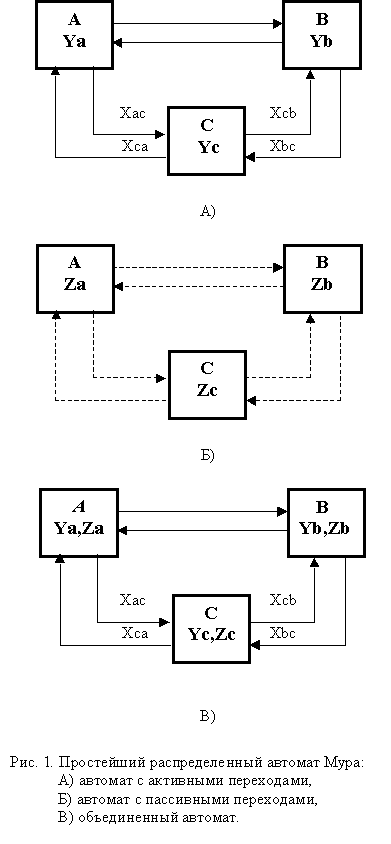
От контроллера в операторскую станцию передается идентификатор состояния, в котором в данный момент пребывает управляющий автомат. По номеру состояния на экран монитора выводится соответствующая информация для оператора. При этом в операторской станции реализуется алгоритм, задаваемый графом переходов автомата с теме же вершинами и дугами, что и в алгоритме контроллера, но без отметок дуг и с новыми отметками вершин (рис. 1Б). При этом идентификаторы состояний совпадают с рис. 1А, но идентификаторы действий уже другие (Za, Zb, Zc) и обозначают соответствующий вывод информации на экран монитора. Кроме того, дуги этого графа переходов указаны пунктиром и не содержат отметок, обозначающих условия перехода. Переходы, соответствующие пунктирным дугам, будем называть внешними, или пассивными, так как они реализуются другим процессом, в котором такие же дуги отмечены условием перехода (эти дуги будем называть активными). Петли на вершинах так же не показаны, и они также пассивные.

Автомат с пассивными дугами (рис. 1Б) работает следующим образом. От контроллера он получает идентификатор очередного состояния, например, “A”, и выполняет соответствующее ему действие, то есть выводит на экран информацию Za. Когда от контроллера будет получен идентификатор нового состояния, например, “B”, то реализуется пассивный переход из состояния A в состояние B, и автомат формирует действие Zb, пребывая уже в новом состоянии В, и так далее.

В целом, оба указанных алгоритма могут быть объединены в один алгоритм, задаваемый объединенным графом переходов (рис. 1В), в котором вершины отмечены объединением соответствующих отметок вершин графов (рис. 1А, 1Б). При этом полученный граф содержит только активные дуги, помеченные так же, как в автомате контроллера.

Декомпозицию автомата (рис. 1) будем называть распределенным автоматом (РА). В частности рис. 1 демонстрирует простейший РА Мура. В табл. 1 представлена работа этого РА.

Таблица 1

3. Простейшие распределенные автоматы Мили и распределенные С-автоматы

Примечание. С-автомат - это конечный автомат, совмещающий как автомат Мура, так и автомат Мили. То есть, вершины помечены буквами выходного алфавита автомата Мура, а переходы - буквами выходного алфавита автомата Мили. В общем случае алфавиты различимы [4].

Рассмотрим тот же пример с контроллером и операторской станцией, но в случае, когда алгоритм РА задается автоматом Мили (рис. 2). При этом алгоритм контроллера содержит только активные переходы, а алгоритм операторской станции, соответственно, только пассивные переходы. Алгоритм контроллера представляет собой обычный автомат Мили (рис. 2А) и поэтому не представляет интереса. Отметим, что Xaa является отрицанием дизъюнкции “Xab | Xac”.

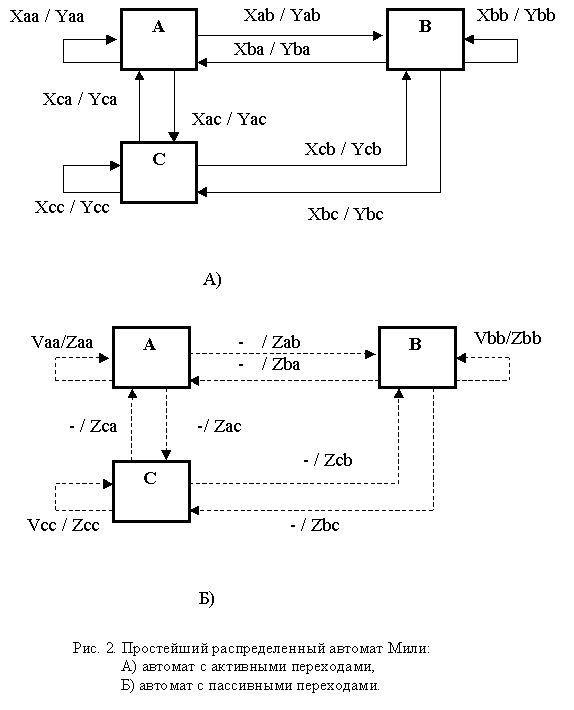
Алгоритм операторской станции на данном примере рассмотрим подробнее. Пассивные переходы в нем осуществляются так же, как и в предыдущем примере, но с тем отличием, что эти переходы могут иметь свои отметки. В рассматриваемом случае (рис. 2Б) переходы между состояниями отмечены действиями, выполняемыми операторской станцией при изменении состояния автомата, реализуемого контроллером. Например, при переходе из состояния А в состояние В выполняется действие Zab (безусловно). Однако отметки на пассивных дугах могут иметь и условия, действительные только для операторской станции. В данном случае такие отметки размещаются на пассивных петлях. Например, петля у вершины А помечена условием Vaa и соответствующим действием Zaa. Это означает, что пока автомат, реализуемый контроллером, пребывает в состоянии А, в это время автомат, реализуемый операторской станцией, проверяет некоторое условие Vaa, и при его выполнении производится действие Zaa; при невыполнении указанного условия никаких действий не производится. Таким образом, состояние А имеет по существу две петли: одна показана на рисунке, а вторая, помеченная отрицанием Vaa и не помеченная ни каким действием, на рисунке не показана и подразумевается по умолчанию.

В принципе число однонаправленных дуг (петель), исходящих из одной вершины и помеченных различными условиями и/или действиями, может быть произвольным, что превращает граф переходов в мультиграф [3].

На рис. 3 изображен в качестве примера распределенный С-автомат с алгоритмом работы контроллера (рис. 3А) и операторской станции (рис. 3Б). Рассмотрим работу контроллера. В исходном состоянии А автомата контроллера ожидается выполнение условия x, свидетельствующего, например, о принадлежности значения контролируемой величины заданному диапазону. При наличии x автомат переходит в состояние В с одновременным обнулением счетчика t программных циклов. Из состояния В автомат возвращается в исходное состояние при исчезновении условия x. При сохранении x в каждом программном цикле состояния В счетчик увеличивается на единицу (t++). Если значение счетчика превысит заданный порог Т, то автомат переходит в состояние С, из которого возвращается в исходное только при исчезновении условия x.

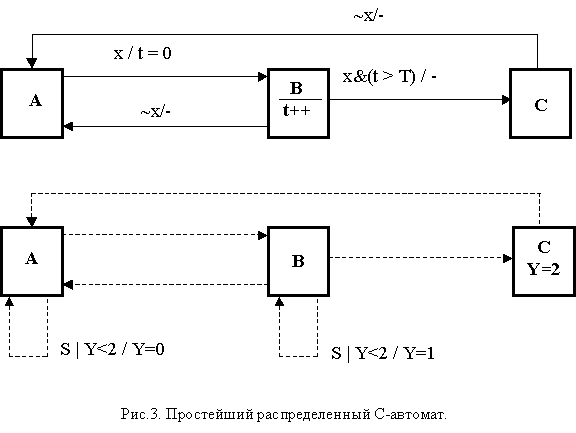
Перейдем к описанию работы автомата операторской станции. Как и в предыдущих примерах этот автомат содержит только пассивные дуги (петли), то есть отслеживает переходы из состояния в состояние автомата контроллера. Основная задача автомата операторской станции в данном примере заключается в установке значения переменной Y, обозначающей, например, цвет выводимого на экран значения контролируемой величины, получаемой из контроллера (наряду с идентификатором состояния). В состоянии С указанная переменная всегда принимает значение 2. Состояния А и В имеют по две петли (на рисунке показаны только по одной из двух – см. выше). Условия, помечающие петли данных вершин, одинаковы и на рис.3,Б имеют вид дизъюнкции: условие S (сброс) или значение переменной Y меньше двух. Но при выполнении условия “S | Y<2” в состоянии А переменная Y устанавливается равной нулю, а в состоянии В – единице. Таким образом автомат операторской станции определяет цвет выводимой на экран области: например, в состоянии С – красный, в состоянии В – желтый, в состоянии А – зеленый; при этом желтый и зеленый цвета устанавливаются либо по сбросу либо в том случае, когда не установлен красный цвет.

Все вышеописанные РА названы простейшими потому, что представляют пару автоматов, из которых один содержит только активные дуги и определяет все переходы, а второй содержит только пассивные дуги и отслеживает состояния первого безусловно.

4. Асинхронные распределенные автоматы

РА общего вида будем называть такую декомпозицию автоматов, в которой каждый автомат – компонент включает как активные так и пассивные дуги в произвольном сочетании, в том числе и мультидуги.

На рис. 4 представлен пример такого РА, состоящего из трех С-автоматов – компонент. Использованы следующие обозначения. Pab, Pcb, Pca - условия собственных переходов первого автомата (рис. 4,А); Zaa, Zab, Zac,… - действия на вершинах и дугах первого автомата (петли на рисунке опущены); идентификаторы, начинающиеся с Q и Y – соответственно, условия собственных переходов и действия на вершинах и дугах второго автомата (рис. 4,Б); идентификаторы, начинающиеся с R и V – соответственно, условия собственных переходов и действия на вершинах и дугах третьего автомата (рис.4,В). Идентификаторы вида Sij обозначают факт перехода i-го автомата (i = 1,2,3) в j-е состояние (j = a,b,c).

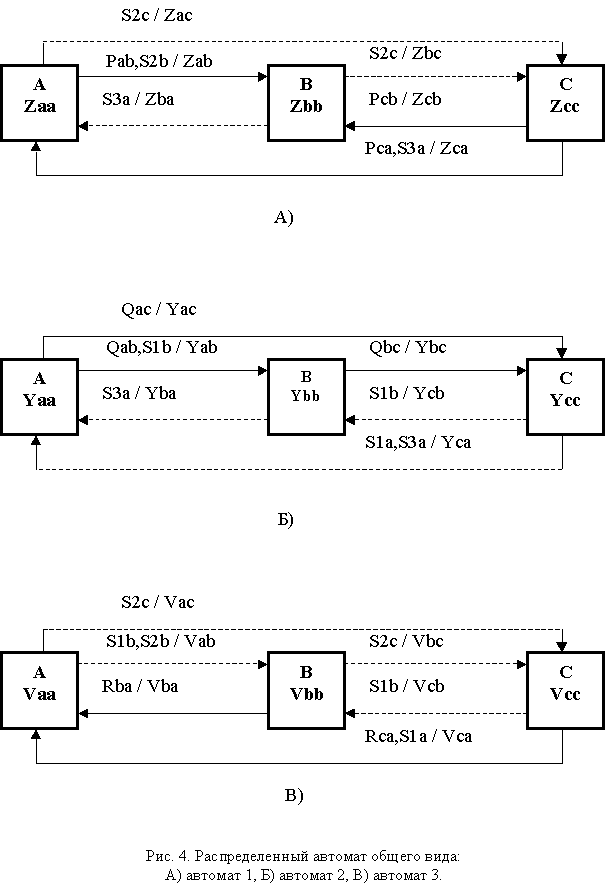
Активную дугу, отмеченную сплошной линией, будем называть собственным переходом i-го автомата, а пассивную дугу, отмеченную пунктиром, будем называть также вынужденным переходом. Если два и более автомата имеют одинаковые собственные переходы, то каждому из этих переходов соответствует мультидуга, включающая как собственный так и вынужденный переходы. На рис. 4 мультидуги показаны сплошной линией, помеченной разделенными запятой условием собственного перехода и обозначением нового состояния другого автомата, то есть условием пассивного (вынужденного) перехода.

Вынужденные переходы помечены разделенными запятой состояниями других автоматов.

Рассмотрим работу РА (рис. 4). Пусть исходным состоянием всех трех автоматов будет состояние А. Автоматы выполняют действия, соответственно, Zaa, Yaa, Vaa. Не вдаваясь в детали программной реализации отметим, что каждый автомат имеет информацию о состоянии каждого другого автомата. Полагаем также, что одновременно не могут иметь место два или более собственных переходов автоматов, то есть переход в новое состояние инициируется единственным автоматом.

Пусть в некоторый момент времени выполнено условие Pab. При этом автомат 1 переходит в состояние В исполняя действие Zab. Этот факт становится известным двум другим автоматам, то есть активизируется переменная S1b в них. Поэтому во втором и в третьем автоматах осуществляется вынужденный переход в состояние В с одновременной реализацией действий, соответственно, Yab и Vab. Далее автоматы пребывают в состоянии В, выполняя действия Zbb, Ybb, Vbb, ожидая дальнейших событий. Пусть следующим событием является появление условия Qbc. При этом второй автомат осушествляет собственный переход из состояния В в состояние С с исполнением действия Ybc. Два другие автомата получают уведомление о переходе в виде активизации переменной S2c и реализуют вынужденный переход из состояния В в состояние С с исполнением действий на переходе, соответственно, Zbc и Vbc. После этого все три автомата пребывают в состоянии С и реализуют соответствующие действия Zcc, Ycc, Vcc. Переход из состояния С возможен теперь при наступлении одного из следующих событий: выполняется условие Pcb или Pca для первого автомата, или выполняется условие Rca для третьего автомата, после чего реализуется соответствующий собственный и два вынужденных перехода как описано выше.

Напомним, что автоматы, составляющие композицию РА, работают как независимые процессы и обмениваются друг с другом (например по сети) только идентификатором состояния после собственного перехода. Такие РА можно называть также асинхронными. В асинхронных РА недопустимо одновременное появление условий, ведущих к осуществлению собственных переходов более чем в одном автомате.

Если РА не удовлетворяет последнему условию, то необходим аппарат разрешения конфликтов.

5. Синхронные распределенные автоматы

Для разрешения конфликта, возникающего при одновременной реализации двух противоречивых собственных переходов, необходим процесс – арбитр. Если в асинхронном РА каждый автомат-компонент отправлял каждому другому компоненту идентификатор своего нового состояния и принимал аналогичные сообщения ото всех других компонент, то при наличии процесса-арбитра – дополнительного автомата-компонента – сообщения о новом состоянии компонент отправляются только арбитру, который, в свою очередь посылает сообщение о своем новом состоянии всем компонентам. Поэтому такие РА будем называть синхронными.

Для разрешения вышеописанных конфликтов во все автоматы-компоненты РА вводятся дополнительные состояния, которые будем называть состояниями синхронизации. На рис. 5,А представлен фрагмент РА, а именно: фрагменты двух автоматов-компонент с конфликтными переходами из состояния А. (Справа в скобках указаны номера компонент.)

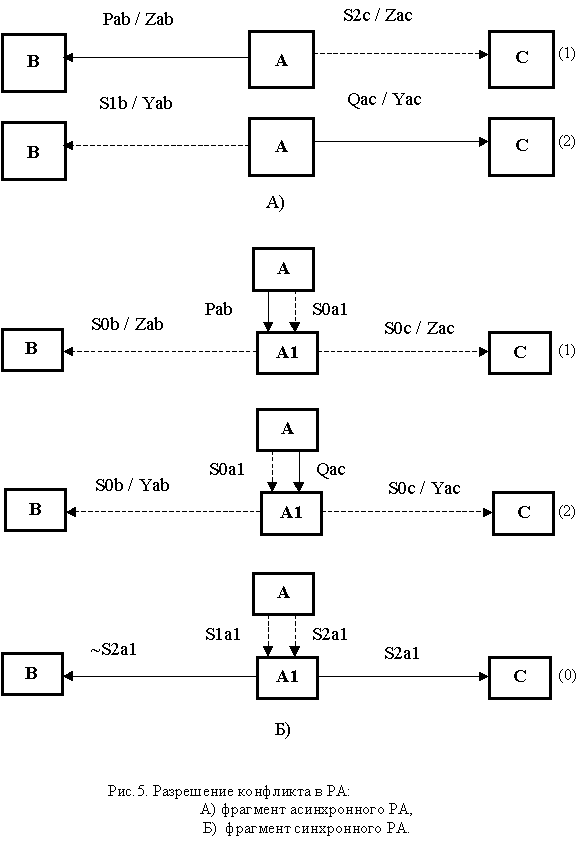
Если РА (рис.5,А) пребывает в состоянии А, то при одновременном выполнении условий Pab и Qac первый автомат перейдет в состояние В, а второй – в состояние С, и РА окажется не работоспособным (вернее все будет зависеть от порядка временной реализации обмена сообщениями).

Для преобразования этого РА в синхронный во-первых вводится дополнительное состояние синхронизации с идентификатором А1, а во-вторых добавляется автомат-арбитр с номером 0 (рис.5,Б). Рассмотрим работу синхронного РА на данном примере.

Пусть РА находится в состоянии А. При выполнении условия Pab и невыполнении условия Qac первый автомат перейдет в состояние А1 и сообщит об этом нулевому автомату-арбитру. Последний запоминает номер автомата, первым перешедшим в состояние А1, и после этого передает сообщение о пребывании в состоянии А1 всем остальным автоматам, и РА в целом будет находиться в этом состоянии. Затем арбитр решает, в какое из двух состояний В или С перевести РА. Для этого в данном примере проверяется первым ли перешел в состояние А1 второй автомат (условие S2a1). В данном случае это не так, и выполняется собственный переход в состояние В, о чем немедленно сообщается другим компонентам РА. После этого другие автоматы осуществляют вынужденный переход в состояние В с реализацией соответствующих действий (Zab, Yab). Идентично работает РА пребывая вначале в состоянии А при выполнении условия Qac и невыполнении условия Pab.

Перейдем к рассмотрению случая, когда, пребывая в состоянии А, РА получает одновременно признаки выполнения условий как Pab так и Qac. При этом как первый так и второй автоматы осуществляют собственные переходы в состояние А1 без реализации каких-либо действий. Арбитр одновременно получает информацию об этом новом состоянии от обоих автоматов и устанавливает соответствующий признак S2a1. Одновременно арбитр осуществляет вынужденный переход в состояние А1, затем сообщает это новое состояние всем компонентам РА, и последний переходит в состояние А1. Далее арбитр согласно признаку S2a1 осуществляет собственный переход в состояние С, о чем и сообщает всем компонентам РА, и последний встает в состояние С. При этом как первый так и второй автоматы реализуют действия Zac и Yac на вынужденных переходах из состояния А1 в состояние С. Таким образом разрешается конфликт, в данном примере в пользу состояния С.

Отметим, что арбитр может использовать произвольные условия разрешения конфликтов, в том числе посредством вмешательства оператора.

6. Заключение

Распределенные автоматы удобно описывают сложные алгоритмы управления распределенными технологическими процессами, когда управление организуется посредством сети, связывающей несколько контроллеров и одну или несколько операторских станций.

Описанный подход годится как для управления “медленными” технологическими процессами, когда одновременное появление двух и более событий практически исключено (асинхронные РА), так и для управления “быстрыми” процессами с применением синхронных РА.

Рассмотренная модель РА не является исчерпывающей и ждет дальнейших исследований.

СПИСОК ЛИТЕРАТУРЫ

1. Лазарев В.Г., Пийль Е.И. Синтез управляющих автоматов – М.: Энергоатомиздат, 1989.
2. Автоматное управление асинхронными процессами в ЭВМ и дискретных системах. /Под ред. В.И.Варшавского. – М.: Наука, 1986.
3. Мелихов А.Н. Ориентированные графы и конечные автоматы. – М.: Наука, 1971.
4. Баранов С.И. Синтез микропрограммных автоматов. - Л.: Энергия, 1979.