Процедурно-параметрическое программирование

Содержание

• Резюме
• Параметрическая обработка альтернатив
• Моделирование параметрического подхода
  • Конструирование параметрического обобщения
  • Создание экземпляров параметрического обобщения
  • Построение обработчиков параметрических обобщений
  • Да ведь это уже было!
  • Параметрический полиморфизм
• Программные объекты процедурно-параметрической парадигмы
• Языковая поддержка параметрического полиморфизма
  • Реализация параметрического обобщения
  • Реализация параметрических процедур
  • Реализация обработчиков параметрических специализаций
  • Создание экземпляров параметрических обобщений
  • Присваивание экземпляров параметрических обобщений
• Новая парадигма. Ну и что?
  • Расширение функциональности параметрических обобщений
  • Добавление специализированных действий
  • Игра на поле соперника. Строим новые альтернативы
  • Наращивание бицепсов агрегатов
• Немного формализма
  • Организация параметрических обобщений
  • Организация обобщающих параметрических процедур
  • Организация обработчиков параметрических специализаций
  • Экземпляр параметрического обобщения
  • Вызовы параметрических процедур
  • Что в результате?
• Подведение итогов
• Заключение
• Историческая справка

Текст статьи можно загрузить из архива (53 кб)

Процедурно-параметрическое программирование

© 2001 А.И. Легалов

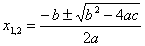
Посвящается методу вычисления действительных корней квадратного уравнения ax2+bx+c=0

Резюме

Предлагается парадигма, определяющая новый стиль разработки программ, названный процедурно-параметрическим программированием (ППП). В ее основе лежит параметрический полиморфизм, позволяющий процедурам принимать и обрабатывать вариантные типы данных без дополнительного алгоритмического анализа. Подход является развитием методов процедурного программирования и может служить альтернативой объектно-ориентированному стилю.

Параметрическая обработка альтернатив

Сравнение процедурного и объектного подходов, представленное в предыдущих заметках по парадигмам программирования, показывает, что основное конструктивное различие проявляется в принципах построения и анализа обобщений. Метод, используемый в ООП, позволяет, в большинстве случаев, расширять код и данные без изменения ранее написанных процедур. Процедурный подход вынуждает, в этих ситуациях, модифицировать фрагменты кода, осуществляющего анализ альтернатив. Вот, если бы, вытащить этот код из процедур, осуществляющих обработку обобщений... Тогда можно повысить возможности процедурного подхода по разработке эволюционно наращиваемых программ.

Вместе с тем, кроме ранее рассмотренных способов, существует еще один метод вычисления F(D), который можно использовать в процедурном программировании. Установить функциональную зависимость между обработчиком специализации f_i и типом специализации t_j можно не только алгоритмически, но и таблично. Такая однозначная зависимость, назовем ее параметрической, может быть показана не фрагментом кода, а таблицей, реализация которой может быть выполнена с использованием двумерного массива:

Доступ к обработчикам специализации, размещенным в таблице, может быть реализован с указанием индексов строки и столбца. Использование параметрической зависимости между процедурами и обобщениями позволяет убрать код из анализа альтернатив и обеспечивает независимость одного аргумента от другого. В представленном случае процедуры перестают зависеть от данных, которые, в свою очередь тоже не зависят от процедур. Такой подход составляет основу параметрического полиморфизма и процедурно-параметрической парадигмы программирования. Для табличного доступа не имеет значения, в какой последовательности определяются и используются индексы элемента. Реализация языковой надстройки для построения механизма выбора альтернатив с применением параметров позволяет получить еще один способ написания кода.

Моделирование параметрического подхода

Параметрический подход можно смоделировать, используя процедурное программирование. Ниже представлена еще одна программа, манипулирующая геометрическими фигурами в соответствии с ранее поставленным условием.

Конструирование параметрического обобщения

Для того, чтобы иметь возможность обрабатывать значения типов без использования механизма их идентификации во время выполнения, введем перечислимый тип данных, каждое значение которого соответствует одной из альтернатив:

То есть, моделирование структуры параметрического обобщения строится точно таким же банальным образом, как и в процедурном подходе.

// Использование параметрического обобщения, построенного на
// основе косвенного альтернативного связывания специализаций.
// Структура, обобщающая все имеющиеся фигуры

struct shape {
    // значения локальных ключей для каждой из фигур
    enum key {RECTANGLE=0, TRIANGLE=1};
    key k; // ключ
    // используется универсальный указатель
    void *s; // подключается любая специализация
};

// Сигнатуры требуемых функций можно тоже подключить через
// заголовочный файл. Но, для простоты, можно и так описать.

rectangle *Create_rectangle(int x, int y);
triangle  *Create_triangle(int a, int b, int c);

//------------------------------------------------------------------
// Динамическое создание обобщенного прямоугольника
shape *Create_shape_rectangle(int x, int y)
{
    shape *s = new shape;
    s->k = shape::key::RECTANGLE;
    s->s = (void*)Create_rectangle(x, y);
    return s;
}

//------------------------------------------------------------------
// Динамическое создание обобщенного треугольника

shape *Create_shape_triangle(int a, int b, int c)
{
    shape *s = new shape;
    s->k = shape::key::TRIANGLE;
    s->s = (void*)Create_triangle(a, b, c);
    return s;
}

//------------------------------------------------------------------
// Инициализация обобщенного прямоугольника

void Init_rectangle(shape &s, int x, int y)
{
    s.k = shape::key::RECTANGLE;
    // Необходимо создать прямоугольник, так как
    // он формируется динамичиески.
    s.s = (void*)Create_rectangle(x, y);
}

//------------------------------------------------------------------
// Инициализация обобщенного треугольника

void Init_triangle(shape &s, int a, int b, int c)
{
    s.k = shape::key::TRIANGLE;
    // Необходимо создать треугольник, так как
    // он формируется динамичиески.
    s.s = (void*)Create_triangle(a, b, c);
}

//------------------------------------------------------------------

Следует отметить использование процедур, ранее написанных для создания отдельных специализаций.

Построение обработчиков параметрических обобщений

Процедуры, обеспечивающие вывод и вычисление площади обобщенной фигуры поддаются параметризации. Кроме этого, используя аналогичный подход, можно создать и процедуру очистки обобщения от значения. Механизм создания таких процедур достаточно прост. Формируются массивы указателей на обработчики специализаций, имеющие одинаковые сигнатуры. Каждый обработчик специализации осуществляет манипуляции с конкретной фигурой, доступ к которой осуществляется путем явного приведения типа. Таблица, описывающая параметризируемые функции данной программы, будет выглядеть следующим образом:

Вот, каким образом можно построить процедуру, осуществляющую очистку обобщенной фигуры.

//------------------------------------------------------------------

// Обработчик, предназначенный для удаления прямоугольника.
// Используется как элемент параметрического массива в процедуре
// очистки обобщенной фигуры.
void Delete_rectangle(shape &s)
{
    delete (rectangle*)s.s;
}

//------------------------------------------------------------------

// Обработчик специализации, предназначенный для удаления треугольника.
// Используется как элемент параметрического массива в процедурах
// очистки обобщенной фигуры.
void Delete_triangle(shape &s)
{
    delete (triangle*)s.s;
}

//------------------------------------------------------------------

// Очистка обобщенной фигуры удалением специализации.
// Остается только "голова" обобщения, которая может
// повторно инициализироваться любым значением.
// Используется параметрический массив.указателей на процедуры
// удаления специализаций.
void (*Clear_shape[])(shape &s) =
    {&Delete_rectangle, &Delete_triangle};

//------------------------------------------------------------------
// Дополнительное переопределение процедуры очистки фигуры,
// сделанное для сокрытия ее реального вида.
// Может отсутствовать.
void Clear(shape &s)
{
    Clear_shape[s.k](s);
}

//------------------------------------------------------------------

Сформированная в конце процедура очистки void Clear(shape &s) показывает, каким образом можно инкапсулировать доступ к параметрическому массиву. Тем самым скрывается один из недостатков моделирования параметрического обобщения: дважды в списке параметров осуществляется обращение к одному и тому же объекту.

//------------------------------------------------------------------
// Сигнатуры требуемых функций можно тоже подключить через
// заголовочный файл. Но, для простоты, можно и так описать.

void Out(rectangle &r);
void Out(triangle &t);

//------------------------------------------------------------------
// Обработчик специализации, предназначенный для вывода параметров
// прямоугольника. Используется как элемент параметрического массива
// в процедуре вывода параметров обобщенной фигуры.

void Out_rectangle(shape &s)
{
    Out(*((rectangle*)s.s));
}

//------------------------------------------------------------------
// Обработчик специализации, предназначенный для вывода параметров
// треугольника. Используется как элемент параметрического массива
// в процедуре вывода параметров обобщенной фигуры.

void Out_triangle(shape &s)
{
    Out(*((triangle*)s.s));
}

//------------------------------------------------------------------
// Нахождение площади обобщенной фигуры.
// Используется параметрический массив.указателей на процедуры
// вычисления площадей специализаций.

void (*Out_shape[])(shape &s) =
    {&Out_rectangle, &Out_triangle};


//------------------------------------------------------------------
// Дополнительное переопределение процедуры вычисления площади
// обобщенной фигуры, сделанное для сокрытия ее реального вида.
// Может отсутствовать.

void Out(shape &s)
{
    Out_shape[s.k](s);
}

//------------------------------------------------------------------

//------------------------------------------------------------------
// Сигнатуры требуемых функций можно тоже подключить через
// заголовочный файл. Но, для простоты, можно и так описать.

double Area(rectangle &r);
double Area(triangle &t);

//------------------------------------------------------------------
// Обработчик специализации, предназначенный для вычисления площади
// прямоугольника. Используется как элемент параметрического массива
// в процедуре вычисления площади обобщенной фигуры.

double Area_of_rectangle(shape &s)
{
    return Area(*((rectangle*)s.s));
}

//------------------------------------------------------------------
// Обработчик специализации, предназначенный для вычисления площади
// треугольника. Используется как элемент параметрического массива
// в процедуре вычисления площади обобщенной фигуры.

double Area_of_triangle(shape &s)
{
    return Area(*((triangle*)s.s));
}

//------------------------------------------------------------------
// Нахождение площади обобщенной фигуры.
// Используется параметрический массив.указателей на процедуры
// вычисления площадей специализаций.

double (*Area_of_shape[])(shape &s) =
    {&Area_of_rectangle, &Area_of_triangle};


//------------------------------------------------------------------
// Дополнительное переопределение процедуры вычисления площади
// обобщенной фигуры, сделанное для сокрытия ее реального вида.
// Может отсутствовать.

double Area(shape &s)
{
    return Area_of_shape[s.k](s);
}

//------------------------------------------------------------------

Исходный текст программы, моделирующей параметрическое обобщение, приведен в архиве pp_examp1p.zip.

Да ведь это уже было!

Приведенный метод обработки альтернатив не является моим величайшим открытием. Он издавна используется в практике процедурного программирования и даже намного чаще, чем имитация объектно-ориентированного подхода, так как менее громоздок при тех же результатах. У Страуструпа [Страуструп] он описан при демонстрации указателей на функции. Ясно также, что непосредственное использование таких приемов не повысит шансов процедурного программирования в борьбе с ОО стилем. Ведь поиск и обнаружение ошибок в программе необходимо осуществлять во время ее выполнения. Однако приведенный пример указывает путь по дальнейшему языковому расширению процедурного подхода. И здесь я готов отстаивать свое первенство на предлагаемые решения.

Параметрический полиморфизм

Посмотрев еще раз на рисунок, демонстрирующий особенности динамического формирования альтернатив в объектном обобщении (рис. 1), мы увидим, что множество процедур, осуществляющих обработку некоторой специализации, размещаются в единой таблице виртуальных функций. Из рисунка также видно, что одна и та же обобщающая процедура F_i "размазана" по различным таблицам, но, при этом, в каждой из них находится в одной и той же позиции.

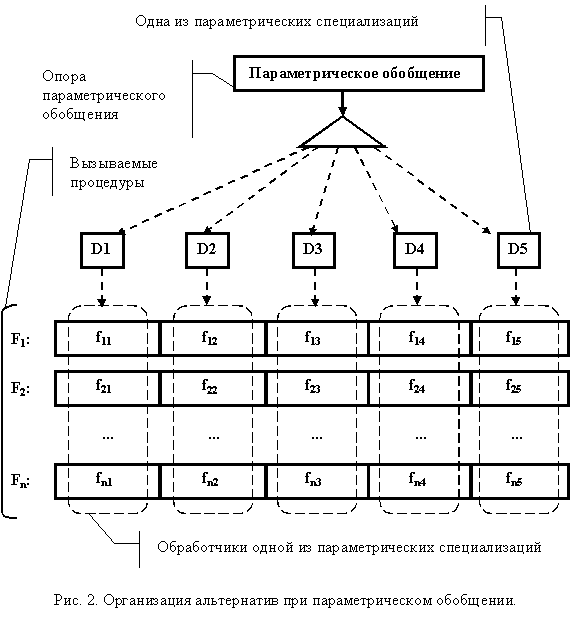
Теперь посмотрим на то, как организованы структуры данных, используемые при формировании параметрического обобщения (рис. 2). Все правильно! Перпендикулярно, точнее, ортогонально! Так всегда и происходит при сопоставлении процедурного подхода с объектным! Специализации, реализующие одну обобщающую процедуру, оказались собраны в едином массиве. При этом отдельные специализированные процедуры различного назначения, используемые для обработки одной и той же специализации, находятся в разных массивах, но на одной и той же позиции. То есть, отличие только в том, что иначе разрезали матрицу! А раз так, то почему бы ни подыскать такие языковые надстройки над процедурным подходом, которые обеспечивают необходимый синтаксический и семантический контроль ортогонального разрезания на этапе компиляции. Ведь нашли же, в свое время, аналогичную объектно-ориентированную надстройку, создав языки, методологии, религию. Хотя, я думаю, исходные посылки были другими.

По аналогии с ООП, можно говорить о параметрическом полиморфизме как методе, обеспечивающем изменение поведения процедур путем создания отношений между параметрическими обобщениями, объединяющими альтернативные специализации, и обобщающими процедурами, предоставляющими специализированные обработчики для соответствующих комбинаций специализированных данных. В представленной выше программе роль параметрического обобщения выполняет фигура shape. Роль обобщающих "процедур", обеспечивающих полиморфизм, возлагается на массивы указателей Clear_shape, Out_shape, Area_of_shape.

Параметризация процедур может осуществляться по одному или нескольким аргументам, имеющим тип, соответствующий одному из типов, используемому в специализациях параметрических обобщений. В рассматриваемой процедурной программе параметризация реализована с использованием массивов указателей на специализированные функции. Имена массивов указателей служат именами обобщающих функций. Переопределение этих функций, добавленное после объявления массивов, сделано для удобства и сокрытия механизма обобщения. Оно может отсутствовать.

Описанный выше способ написания программ может использоваться как при процедурном, так и функциональном программировании, а также при программировании на уровне процессов, обеспечивая при этом полиморфизм аргументов соответствующих процедур без изменения внутренней организации обобщающей процедуры. А ведь именно необходимость коррекции таких процедур при сопровождении сложных программных систем и явилась причиной заката процедурного программирования, не выдержавшего конкуренции с ООП. Однако, для того, чтобы данный метод мог действительно применяться как парадигма программирования, необходимо разработать соответствующие языковые средства, скрывающие особенности реализации механизма параметрического полиморфизма.

Программные объекты процедурно-параметрической парадигмы

ППП предлагает ряд специфических способов конструирования составных программных объектов, отсутствующих в процедурном и объектном подходах. Прежде чем приступить к описанию воображаемого процедурно-параметрического языка и написанию на нем программ, рассмотрим основные особенности процедурно-параметрической (ПП) парадигмы.

1. Конструирование агрегатов осуществляется так же, как и при процедурном подходе, с использованием тех же структур и внешних процедур. Возможно, если язык поддерживает, применение механизма наследования данных, которые, как предполагается, не содержат встроенных процедур, являющихся неотъемлемой чертой классов (зачем размножать сущности, если процедуры уже имеются снаружи?).
2. Структуры данных, представляющие отдельные специализации обобщения (параметрические специализации), по своим свойствам и назначению полностью эквивалентны вариантным специализациям процедурного подхода. То есть, это обычные и любые типы данных.
3. Обобщения данных строятся с использованием программных объектов, названных параметрическими обобщениями. Они предназначены для группировки параметров, обеспечивающих однозначную связь с соответствующими параметрическими специализациями. Эти программные объекты схожи по структуре с вариантными обобщениями. Однако они несколько отличаются по способам использования.
4. Экземпляры параметрических обобщений, определяющие конкретные специализации, будем называть параметрическими экземплярами.
5. Обобщающие параметрические процедуры (или просто параметрические процедуры) поддерживают механизм параметрического полиморфизма. Они не имеют аналогов в других парадигмах программирования. Их основная задача - описание параметрических аргументов и обработчика по умолчанию. Схожие, но не совпадающие свойства, можно наблюдать у методов базовых классов.
6. Обработчики параметрических специализаций (или параметрические обработчики) - процедуры, осуществляющие непосредственную обработку параметрических специализаций. Их отличие от обработчиков вариантов заключается в использовании, в качестве параметров, не самих специализаций, а параметрических обобщений. Таким образом, все обработчики параметрических специализаций имеют сигнатуру, одинаковую с обобщающей параметрической процедурой. Отличие параметрических обработчиков друг от друга заключается в наличии дополнительных признаков, идентифицирующих специализации, для обработки которых они предназначены

Языковая поддержка параметрического полиморфизма

В работе не ставится задача описания еще одного языка программирования. Ниже предлагаются те конструкции, которые, на мой взгляд, были бы полезны при расширении любого языка программирования средствами представления параметрического полиморфизма. Делается попытка привязки этих конструкций к синтаксису языка программирования C++, используемому в этом материале при написании реальных программ. Следует также отметить, что в представленных примерах раскрываются не все особенности новых языковых конструкций, проработанных к настоящему моменту. Это тема отдельного и весьма длительного разговора. В данных заметках мне хочется донести лишь общую концепцию ППП.

Реализация параметрического обобщения

Параметрическое обобщение должно задавать признаки специализаций. Кроме этого, если с признаком связываются обрабатываемые данные, можно задавать их тип. Вот, каким образом, описывается обобщенная геометрическая фигура.

//------------------------------------------------------------------
// Параметрическое обобщение задается следующим образом:

union shape switch (inline)
{ // для идентификации специализаций используются локальные признаки
    case RECTANGLE: rectangle; // обобщается прямоугольник
    case TRIANGLE:  triangle;  // обобщается треугольник
};

//------------------------------------------------------------------

Используемый в данной работе синтаксис комбинирует ключевые слова из объединения и переключателя. Конечно, возможна и более изящная конструкция. Но я и не претендую на стандартизацию. Однако я попытался использовать как можно меньше новых ключевых слов. Поэтому, ключевое слово C++ inline применяется для указания того, что признаки задаются непосредственно в обобщении, то есть, без использования внешних типов данных. Хотя, в общем, допустимо задавать признаки константными значениями любых типов, для которых определены операции сравнения. Например, можно использовать целые числа. Тогда обобщение будет выглядеть следующим образом:

//------------------------------------------------------------------
// Параметрическое обобщение задается следующим образом:

union shape switch (int) // признаки являются целыми числами
{
    case 4: rectangle; // обобщается прямоугольник
    case 3:  triangle;  // обобщается треугольник
};

//------------------------------------------------------------------

Можно использовать в качестве признаков все значения перечисления или только часть их:

//------------------------------------------------------------------
// Где-то есть перечислимый тип:

enum SHAPE_ID { RECTANGLE, TRIANGLE, CIRCLE };

// Параметрическое обобщение задается следующим образом:

union shape switch (SHAPE_ID) // признаки задаются перечислимым типом
                              // Круг пока не определен
{ // для идентификации специализаций используется тип SHAPE_ID
    case RECTANGLE: rectangle; // обобщается прямоугольник
    case TRIANGLE:  triangle;  // обобщается треугольник
};

//------------------------------------------------------------------

Можно вообще не задавать значения признаков, используя для идентификации специализаций их типы данных. Необходимо только, чтобы все типы в обобщении были различными. Явное наличие признаков позволяет многократно использовать в обобщении один и тот же тип, обеспечивая, тем самым, его различную трактовку.

//------------------------------------------------------------------
// Параметрическое обобщение с уникальными типами:

union shape switch (typeid) // признаки явно не задаются
{
    // для идентификации специализаций используются их типы
    rectangle; // обобщается прямоугольник
    triangle;  // обобщается треугольник
};

//------------------------------------------------------------------

Вот что, примерно, планируется в языке "будущего", а пока излагается на уровне рабочей гипотезы.

В параметрическом обобщении используются ранее написанные специализации. Они точно такие же, как и в процедурном подходе.

//----------------------------------------------------------------

// прямоугольник
struct rectangle {
    int x, y; // ширина, высота
};

//----------------------------------------------------------------

// треугольник
struct triangle {
    int a, b, c; // стороны
};

//----------------------------------------------------------------

Реализация параметрических процедур

Анализ вариантов для уже существующих данных в процедурном подходе осуществлялся при выводе и вычислении площади обобщенной фигуры. Именно эти процедуры и подлежать параметризации. Для процедуры вывода достаточно задать сигнатуру следующим образом:

//----------------------------------------------------------------
// Обобщающая параметрическая процедура, определяющая сигнатуру
// обработчиков параметрических специализаций и, возможно,
// обработчик по умолчанию (здесь - отсутствует)
// Это чистая параметрическа процедура. Требует обязательного
// присутствия всех параметрических обработчиков

void Out[shape &s]() = 0;

//----------------------------------------------------------------

Отсутствие тела у параметрической процедуры говорит о том, что обязательно должны быть явно определены все ее обработчики параметрических специализаций. То есть, по аналогии с чистой функцией абстрактного класса, можем иметь чистую параметрическую процедуру. Однако параметрическая процедура может иметь тело, определяющее обработку по умолчанию тех альтернатив, для которых не создан свой параметрический обработчик. Это тело может также использоваться для генерации исключений в непредусмотренных ситуациях, например:

//----------------------------------------------------------------
// Обобщающая параметрическая процедура, определяющая сигнатуру
// обработчиков параметрических специализаций и
// обработчик по умолчанию

void Out[shape &s]()
{
    throw ShapeExeption;
}

//----------------------------------------------------------------

Можно, также, переопределить сигнатуру параметрической процедуры для сокрытия деталей ее реализации от клиента:

//----------------------------------------------------------------
// Возможно дополнительное переопределение параметрической процедуры
// для сокрытия ее реального вида. Может отсутствовать.

void Out(shape &s)
  {
    Out[s](); // - это вызов параметрической процедуры
  }

//----------------------------------------------------------------

Почему же я сразу не использую для параметрических процедур общую функциональную запись, а выделяю параметрические аргументы в отдельные квадратные скобки. Просто, по ряду субъективных причин, мне захотелось как-то "отметить" этот список. Например, обобщение может использоваться и как обычный аргумент. И тогда, в вызове процедур будет непонятно, в какой роли оно применяется. Хотелось также отдать дань уважения тому методу написания процедурных программ, который привел меня к этой парадигме.

Аналогичным образом строится параметрическая процедура, определяющая вычисление площади обобщенной фигуры:

//----------------------------------------------------------------
// Обобщающая параметрическая процедура, определяющая сигнатуру
// обработчиков параметрических специализаций и, возможно,
// обработчик по умолчанию (здесь - отсутствует)
// Это чистая параметрическа процедура. Требует обязательного
// присутствия всех параметрических обработчиков

double *Area[shape &s]() = 0;

//----------------------------------------------------------------
// Возможно дополнительное переопределение параметрической процедуры
// для сокрытия ее реального вида. Может отсутствовать.

double Area(shape &s)
{
    return Area[s]();
}

//----------------------------------------------------------------

Реализация обработчиков параметрических специализаций

Параметрический обработчик, на основе известной ему сигнатуры параметрической процедуры, определяет тело для обработки конкретной специализации. При этом в нем может вызываться обработчик специализации, написанный еще в те времена, когда о параметрическом обобщении никто и не думал. Вот каким образом обрабатываются специализации обобщенной геометрической фигуры.

//----------------------------------------------------------------
// Сигнатуры функций вывода специализаций

void Out(rectangle &r);
void Out(triangle &t);

//----------------------------------------------------------------
// Параметрический обработчик, предназначенный для вывода
// прямоугольника. Выбирается неявно при обращении к параметрической
// процедуре, если аргумент является прямоугольником

void Out[shape<RECTANGLE> &s]()
{
    Out(s); // s видится транслятору как простой прямоугольник
    // То есть, используется вызов функции void Out(rectangle &r);
}

//----------------------------------------------------------------
// Параметрический обработчик, предназначенный для вывода
// треугольника. Выбирается неявно при обращении к параметрической
// процедуре, если аргумент является треугольником

void Out[shape<TRIANGLE> &s]()
{
    Out(s); // s видится транслятору как простой треугольник
    // То есть, используется вызов функции void Out(triangle &t);
}

//----------------------------------------------------------------
// Сигнатуры функций вычисления площадей специализаций

double Area(rectangle &r);
double Area(triangle &t);

//----------------------------------------------------------------
// Параметрический обработчик, предназначенный для вычисления площади
// прямоугольника. Выбирается неявно при обращении к параметрической
// процедуре, если аргумент является прямоугольником
double Area[shape<RECTANGLE> &s]()
{
    return Area(s); // s видится транслятору как простой прямоугольник
    // То есть, используется вызов функции double Area(rectangle &r);
}

//----------------------------------------------------------------
// Параметрический обработчик, предназначенный для вычисления площади
// треугольника. Выбирается неявно при обращении к параметрической
// процедуре, если аргумент является треугольником
double Area[shape<TRIANGLE> &s]()
{
    return Area(s); // s видится транслятору как простой треугольник
    // То есть, используется вызов функции double Area(triangle &t);
}

//----------------------------------------------------------------

Внутри параметрических обработчиков обобщающая переменная явно идентифицирована заданным типом. Он указан в угловых скобках. Поэтому, транслятор может работать с ней также как и соответствующей специализированной переменной. При написании программы не нужно указывать составных имен.

Создание экземпляров параметрических обобщений

При создании экземпляров параметрических обобщений необходимо сразу указывать специализацию, чтобы в дальнейшем иметь правильную параметрическую привязку. Кроме этого, от признака может зависеть и внутренняя организация переменной (смотрите способы построения вариантов в процедурном подходе). В принципе, ничего сложного здесь нет. Обобщение может создаваться, как и любая переменная: задается тип и имя переменной. Необходимо только, при задании типа, указать признак специализации. Работа с полями переменной осуществляется без каких-либо трудностей. Например:

//----------------------------------------------------------------

shape<RECTANGLE> sr; // экземпляр обобщенного прямоугольника
// Инициализация полей прямоугольника
sr.x = 5; sr.y = 10;

shape<TRIANGLE>  st; // экземпляр обобщенного треугольника
// Инициализация полей треугольника
st.a = sr.x; st.b = 10; st.c = sr.y;

//----------------------------------------------------------------

Обобщенная переменная может быть задана как в глобальном пространстве имен, так и внутри процедур. Принципы ее создания и уничтожения ничем не отличаются от других типов данных. Исходя из этого, можно создавать и экземпляры в динамической памяти:

//----------------------------------------------------------------

// экземпляр обобщенного прямоугольника
shape<RECTANGLE> *srp = new shape<RECTANGLE>;
// Инициализация полей прямоугольника
srp->x = 5; srp->y = 10;

// экземпляр обобщенного треугольника
shape<TRIANGLE>  *stp = new shape<TRIANGLE>;
// Инициализация полей треугольника
stp->a = sr.x; stp->b = 10; stp->c = sr.y;

//----------------------------------------------------------------

Кроме этого, для того, чтобы каждый раз явно не выписывать доступ к полям создаваемых фигур, можно написать соответствующие процедуры создания и инициализации.

//----------------------------------------------------------------
// Динамическое создание обобщенного прямоугольника,
// размещенного в параметрическом обобщении
// с использованием специально созданной функции

shape *Create_shape_rectangle(int x, int y)
{
    shape<RECTANGLE> *s = new shape<RECTANGLE>;
    // Использование конкретизатора для указателя на обобщение
    // позволяет обрабатывать его как указатель только на прямоугольник
    s->x = x;
    s->y = y;
    return s; // При возврате указатель обезличиватеся
}

//----------------------------------------------------------------
// Динамическое создание обобщенного треугольника,
// размещенного в параметрическом обобщении
// с использованием специально созданной функции

shape *Create_shape_triangle(int a, int b, int c)
{
    shape<TRIANGLE> *s = new shape<TRIANGLE>;
    // Использование конкретизатора для указателя на обобщение
    // позволяет обрабатывать его как указатель только на треугольник
    s->a = a;
    s->b = b;
    s->c = c;
    return s; // При возврате указатель обезличиватеся
  }

//----------------------------------------------------------------
// Инициализация обобщенного прямоугольника
// Необходимо явно конкретизировать указатель,
// иначе транслятору не будет видно, что это прямоугольник
void Init_rectangle(shape<RECTANGLE> &s, int x, int y)
{
    s.x = x;
    s.y = y;
}

//----------------------------------------------------------------
// Инициализация обобщенного треугольника
// Необходимо явно конкретизировать указатель,
// иначе транслятору не будет видно, что это треугольник
void Init_triangle(shape<TRIANGLE> &s, int a, int b, int c)
{
    s.a = a;
    s.b = b;
    s.c = c;
}

//----------------------------------------------------------------

Представленные методы создания экземпляров переменных не обладают теми удобствами, которые предоставляют конструкторы классов. Разработчики языков так резко "кинули" процедурное программирование, переключившись на ООП, что не успели оставить после себя эффективных методов инициализации. Хотя, далеко и не надо было ходить. Достаточно использовать метафору приведения типов. В результате можно получить механизм, похожий на конструктор, но размещенный за пределами объекта. Не так трудно аналогичную метафору придумать и для деструктора, если действительно заняться современным процедурно-параметрическим языком. Ниже приводятся примеры процедур приведения типов и их использования при создании переменных.

//----------------------------------------------------------------
// Конструирование прямоугольника (аналог конструктора)

rectangle (int _x, int _y)
{
    x = _x;
    y = _y;
}

//----------------------------------------------------------------
// Конструирование треугольника (аналог конструктора)

triangle (int _a, int _b, int _c)
{
    a = _a;
    b = _b;
    c = _c;
}

//----------------------------------------------------------------
// Конструирование обобщенного прямоугольника, размещенного
// в параметрическом обобщении с использоанием функции
// приведения типа (аналог конструктора)

shape<RECTANGLE> (int _x, int _y)
{
    // Использование конкретизатора позволяет задать
    // создаваемый вариант параметрической специализации
    x = _x;
    y = _y;
}

//----------------------------------------------------------------
// Конструирование обобщенного треугольника, размещенного
// в параметрическом обобщении с использоанием функции приведения
// типа (аналог конструктора)

shape<TRIANGLE>(int _a, int _b, int _c)
{
    // Использование конкретизатора позволяет задать
    // создаваемый вариант параметрической специализации
    a = _a;
    b = _b;
    c = _c;
}

//----------------------------------------------------------------
// Использование процедур приведения при создании экземпляров
//----------------------------------------------------------------

// Инициализированный статический прямоугольник
rectangle r(5, 10);
// Инициализированный статический треугольник
triangle  t(r.x, 10, r.y);
// Динамическое создание и инициализация прямоугольника
rectangle *rp = new rectangle(5, 10);
// Динамическое создание и инициализация треугольника
triangle *tp = new triangle(r.x, 10, rp->y);

//----------------------------------------------------------------

// Инициализированный статический обобщенный прямоугольник
shape<RECTANGLE> sr(5, 10);
// Инициализированный статический обобщенный треугольник
shape<TRIANGLE>  st(sr.x, 10, sr.y);
// Динамическое создание и инициализация обобщенного прямоугольника
shape<RECTANGLE> *srp = new shape(5, 10);
// Динамическое создание и инициализация обобщенного треугольника
shape<TRIANGLE>  *stp = new shape(sr.x, 10, srp->y);

//----------------------------------------------------------------

Примечание. В представленном фрагменте кода возникает противоречие с синтаксисом C, да и C++ тоже. Например, код, описывающий приведение типа, трактуется в C как функция, возвращающая по умолчанию целочисленное значение. Поэтому, я бы и не хотел говорить о реализации подобных конструкций в стандартизованных языках прежде, чем специалисты не выскажут свое мнение и не приведут синтаксис и семантику в соответствие с уже существующим. Для уточнения можно перед функцией приведения ставить ключевое слово, например, typeid:

//----------------------------------------------------------------
// Конструирование прямоугольника (аналог конструктора)

typeid rectangle (int _x, int _y)
{
    x = _x;
    y = _y;
}

//----------------------------------------------------------------

...

//----------------------------------------------------------------
// Конструирование обобщенного прямоугольника, размещенного
// в параметрическом обобщении с использоанием функции
// приведения типа (аналог конструктора)

typeid shape<RECTANGLE> (int _x, int _y)
{
    // Использование конкретизатора позволяет задать
    // создаваемый вариант параметрической специализации
    x = _x;
    y = _y;
}

...

//----------------------------------------------------------------

Присваивание экземпляров параметрических обобщений

Выполнение операции присваивания должно проводится по правилам, обеспечивающим непротиворечивость данных. Нечто подобное происходит и в других языках. Так как в записях содержатся только данные, присваивание по умолчанию для параметрических обобщений может проходить более гибко, чем присваивание классов в ОО языках.

Вот примерный перечень возможных вариантов присваивания выражений "левой части" (lvalue) оператора присваивания.

1. Левой части - указателю на параметрическое обобщение может быть присвоено значение выражения такого же типа или указателя на любой параметрический экземпляр данного обобщения (для которого известен признак). Во втором случае происходит потеря информации о типе. То есть, тип присвоенного значения становится неизвестным. Аналогичная ситуация наблюдается и в ООП при присваивании указателю на базовый класс значения указателя на производный класс.
2. Левой части - указателю на параметрический экземпляр (с известным признаком и, следовательно, структурой) можно присвоить только указатель на однотипный параметрический экземпляр. То есть, специализацию, значение признака которой совпадает с признаком левой части.
3. Экземпляр параметрического обобщения должен всегда иметь конкретное значение признака, задаваемое при его создании. Это означает, что в левой части операции присваивания может быть только параметрический экземпляр.
4. Левой части - параметрическому экземпляру, можно присвоить значение только такого же параметрического экземпляра или значение обычной специализации, тип которого совпадает с типом параметрического экземпляра.
5. Левой части - являющейся некоторым типом данных, может быть присвоено значение параметрического экземпляра только в случае, когда тип этого параметрического экземпляра совпадает с типом левой части.
6. Представленные присваивания могут происходит во время выполнения программы, в ходе начального создания и инициализации переменных, при передаче фактических параметров процедурам. То есть, здесь есть все, что и в других языках программирования.

Возможно, что в этом неформальном описании упущены какие-то моменты. Однако данные правила могут служить основой для более детального обсуждения проблемы. Ниже приводятся примеры, иллюстрирующие правила присваивания.

//----------------------------------------------------------------
// Использование процедур приведения при создании экземпляров
//----------------------------------------------------------------

// Инициализированный статический прямоугольник
rectangle r(5, 10);
// Инициализированный статический треугольник
triangle  t(r.x, 10, r.y);

// Присваивание обобщенному прямоугольнику обычного
shape<RECTANGLE> sr = r;
// Присваивание обычному типу значения параметрического экземпляра
r = sr;
// Присваивание обобщенному треугольнику обычного
shape<TRIANGLE>  st = t;
// Присваивание одному параметрическому экземпляру значения другого
shape<TRIANGLE>  st2 = st;

// А это недопустимо!
// sr = t;
// st = sr;
// t = sr;

// Присваивание обезличенному указателю
// указателя на параметрическую специализацию
shape *sp = &st;
sp = &sr;
shape *sp2 = &sp;

// Присваивание указателю на обобщенный прямоугольник
// только указателя на другой такой же прямоугольник
shape<RECTANGLE> *srp = &sr;

// А здесь - ошибки при работе с указателями!
// shape<TRIANGLE>  *stp = srp;
// shape<TRIANGLE>  *stp = sp;

//----------------------------------------------------------------

Естественно, что я не удержался от соблазна и еще раз переписал свой замусоленный пример на воображаемом процедурно-параметрическом языке. Результаты лежат в архиве ppp_examp1.zip. К сожалению, пока нельзя непосредственно проверить правильность этой гипотетической программы. Поэтому заранее извиняюсь за все имеющиеся в ней ошибки.

Новая парадигма. Ну и что?

Опять встают вполне естественные вопросы: А для чего все это нужно? Что, нам не хватает возможностей ООП? Ответ с философским уклоном гласит: Кому-то хватает, а кому-то нет. Ниже я пытаюсь обосновать свою точку зрения.

Расширение функциональности параметрических обобщений

ППП является прямым расширением процедурного подхода, вбирая, таким образом, все его достоинства. На мой взгляд, они проявляются в более гибком конструировании агрегатов, а также в расширении интерфейса обобщений за счет добавления внешних процедур. Рассмотрим, каким образом изменится процедурно-параметрическая программа, если потребуется добавить вычисление периметра обобщенной фигуры. Будем также считать, что раньше мы это добавление не предусматривали.

//----------------------------------------------------------------
// Вычисление периметра обобщенного прямоугольника
// Параметрическая процедура является чистой,
// что требует яного описания всех специализаций

double Perimetr[shape &s]() = 0;

//----------------------------------------------------------------
// Вычисление периметра для обобщенного прямоугольника

double Perimetr[shape<RECTANGLE> &s]() // s - прямоугольник
{
    return (x + y) * 2.0;
}

//----------------------------------------------------------------
// Вычисление периметра для обобщенного прямоугольника

double Perimetr[shape<TRIANGLE> &s]() // s - треугольник
{
    return a + b + c;
}

//----------------------------------------------------------------

Итак, проблем с добавлением не возникает! В отличие от ООП.

Добавление специализированных действий

Можно также говорить о достаточной гибкости при добавлении специализированных действий. В данной ситуации можно использовать как процедурный подход, так и формирование обобщающей параметрической процедуры, осуществляющей обработку только одной параметрической специализации. Во всех остальных случаях запускается обработчик по умолчанию. Вот что может получиться, если нам захочется выводить только прямоугольники.

//----------------------------------------------------------------
// Вывод только обобщенного прямоугольника
// Параметрическая процедура ничего не делает для всех,
// явно не заданных параметрических обобщений

bool Out_rectangle[shape &s]() { return false; }

//----------------------------------------------------------------
// Прототип функции вывода прямоугольника

void Out(rectangle &r);

//----------------------------------------------------------------
// Вывод данных только для обобщенного прямоугольника

bool Out_rectangle[shape<RECTANGLE> &s]() // s - прямоугольник
{
    Out(s); // Транслятор вызывает метод вывода прямоугольника
    return true;
}

//----------------------------------------------------------------

Можете сравнить, как этот вывод был реализован при процедурном и объектно-ориентированном подходах. Таким образом, процедуры, осуществляющие избирательные действия, реализуются, при ППП, достаточно гибко. Нет никаких изменений интерфейсов, как это происходит при ООП. Не надо также вторгаться во внутренности обобщающей процедуры при добавлении альтернатив, столь болезненном при процедурном программировании. Последняя ситуация может возникнуть, например, в том случае, если нам захочется добавить в программу квадрат в виде специальной фигуры, а затем вывести его, как один из вариантов прямоугольника.

Игра на поле соперника. Строим новые альтернативы

Рассмотрев, как в ППП реализуются плюсы процедурного программирования, перейдем к минусам, самым большим из которых является проблема добавления новых альтернатив. Пусть, как и раньше, такой альтернативой будет круг. Ясно, что круг необходимо задать, а потом добавить к обобщению. В простейшем случае это можно сделать путем следующего изменения:

//----------------------------------------------------------------
// В программу добавляется круг

struct circle {
    int r; // радиус
};

//------------------------------------------------------------------
// Параметрическое обобщение изменяется из-за добавления круга

union shape switch (inline)
{ // для идентификации специализаций используются локальные признаки
    case RECTANGLE: rectangle; // обобщается прямоугольник
    case TRIANGLE:  triangle;  // обобщается треугольник
    case CIRCLE:    circle;    // обобщается добавленный круг
};

//------------------------------------------------------------------

После этого можно спокойно создавать новые параметрические обработчики обобщенного круга, без внесения в программу каких-либо дополнительных изменений. Если непосредственное использование круга не требуется, можно даже не создавать отдельные специализированные процедуры для работы с ним (а можно их и сделать).

//----------------------------------------------------------------
// Параметрический обработчик, предназначенный для вывода
// круга. Выбирается неявно при обращении к параметрической
// процедуре, если аргумент является кругом

void Out[shape<CIRCLE> &s]()
{
    // s видится транслятору как простой круг
    cout << "It is Circle: r = " << s.r << endl;
}

//----------------------------------------------------------------
// Параметрический обработчик, предназначенный для вычисления площади
// круга. Выбирается неявно при обращении к параметрической
// процедуре, если аргумент является кругом
double Area[shape<CIRCLE> &s]()
{
    // s видится транслятору как простой круг
    return 3.14159265 * s.r * s.r;
}

//----------------------------------------------------------------

Думаю, что прогресс, по сравнению с процедурным подходом, налицо. Нет никаких переопределений альтернативного кода. Только добавление нового.

Однако, в эту бочку меда сделана попытка влить ложку дегтя. Недостатком является изменение параметрического обобщения, связанное с добавлением новой специализации. Но нейтрализация этого недостатка была решена еще в процедурном подходе. Вирт, в первом Обероне [Wirth], решил проблему за счет наследования данных, правда, в сочетании с обработкой альтернатив, оставшейся внутри процедур. Легко это можно сделать и при программировании на любом процедурном языке, если воспользоваться образным восприятием для построения вариантного обобщения.

Вместе с тем, никто не обязывает нас записывать параметрическое обобщение в виде единой конструкции. Мы можем просто создавать и использовать его отдельные части в разных местах программы, осуществляя окончательную сборку на этапе компоновки или даже выполнения. Вот как может выглядеть процесс формирования и использования такого обобщения для ранее описанного примера. В начале мы можем описать не все параметрическое обобщение, а только его заголовочную часть:

//------------------------------------------------------------------
// Заголовок параметрического обобщения,
// расширяемый по мере надобности

union shape switch (inline);

//------------------------------------------------------------------

Уже здесь можно создавать обобщающие параметрические процедуры, обеспечивающие обработку, непосредственно не связанную с конкретными специализациями. Например:

//------------------------------------------------------------------

void Out[shape &s]() = 0;
double *Area[shape &s]() = 0;

...

//------------------------------------------------------------------

В другом модуле, или далее по тексту текущего модуля, можно использовать этот заголовок и добавить к обобщению информацию об одной или нескольких специализациях.

//------------------------------------------------------------------

shape + // Добавляется прямоугольник
{ case RECTANGLE: rectangle; // обобщается прямоугольник };

// Далее могут следовать обработчики обобщенного прямоугольника
...

//------------------------------------------------------------------

shape + // Добавляются треугольник и круг
{
  case TRIANGLE: triangle; // обобщается треугольник
  case CIRCLE:   circle;   // обобщается круг
};

// Далее могут следовать обработчики обобщенного треугольника
// и обобщенного круга
...

//------------------------------------------------------------------

В дальнейшем аналогичным образом можно добавить и прочие фигуры, расширяя программу и не модифицируя ранее написанный код. Собрать затем все это воедино не составить труда. Уже сейчас я могу назвать не менее пяти способов. Если вы думаете, что такой подход является чем-то новым, то ошибаетесь. Компоновка компиляция и прочие "услуги" настолько перемешались друг с другом, что трудно говорить о каких-то стандартных вариантах. Кстати, у того же Страуструпа [Страуструп2000] в "Дизайне и эволюции..." приводится аналогичный пример сборки множества одинаковых таблиц виртуальных функций в одну на этапе компоновки.

Конечно, синтаксис, используемый в данном примере, вновь не является вершиной совершенства. Но мне кажется, что суть идеи достаточно прозрачна: параметрическое обобщение и его внешние обработчики ничем не уступают объектному обобщению при добавлении новых альтернатив.

Наращивание бицепсов агрегатов

Интересно также посмотреть и на то, каким образом параметрические обобщения могут использоваться при замене агрегатов, чтобы клиент не знал об этом. ООП предлагает наследование и переписывание виртуальных процедур. Основной плюс в том, что новый агрегат может модифицироваться самым произвольным образом. ППП, в общем-то, предлагает аналогичный механизм.

Единственным его узким местом является то, что мы должны предусмотреть подмену агрегата при проектировании программы, предоставив клиенту связь с ним через параметрическое обобщение. А далее все так же, как и при добавлении новых альтернатив. Однако, и ООП страдает таким же недостатком. Связь предоставляется через базовый класс, в котором мы заранее должны предусмотреть виртуализацию методов, чтобы в дальнейшем переопределить их при построении нового агрегата. Так что, и здесь процедурно-параметрический подход ничем не уступает. А в добавлении к агрегату новых методов даже превосходит.

Встает вопрос: а что делать, если возможность подмены агрегата оказалась непредусмотренной? Тогда любая из рассматриваемых парадигм позволяет использовать следующий простой и эффективный метод: заменить существующий агрегат и методы его обработки новыми, а все имена оставить старыми. Работает железно.

Немного формализма

Ниже я еще раз пересказываю текст, написанный выше.

Организация параметрических обобщений

Параметрическое обобщение позволяет сгруппировать в единое понятие не связанные ранее программные объекты, однозначно сопоставляя их с признаками. Признак - это ключ, идентифицирующий программный объект в рамках рассматриваемого контекста, задающего некоторую категорию. Множество признаков:

T = {t₁, t₂, … , t_i, … , t_n} ,

где n - количество признаков используемых для построения параметрического обобщения. Каждому t_i ставится в соответствие специализация

S_j = {s_j1, s_j2, … , s_jq, … , s_jk} ,

где S_j - программный объект, выступающий в роли специализации обобщения. S_j М S, множеству программных объектов, используемых в качестве специализаций обобщения. Множество {s_j1, s_j2, … , s_jq, … , s_jk} - это значения, принимаемые специализацией S_j.

Параметрическое обобщение задается отображением U: TґS, где u_i = (t_i, S_j) определяет отдельный элемент параметрического обобщения. При этом ЅTЅіЅSЅ, то есть, различным признакам могут ставиться в соответствие одинаковые программные объекты, определяющие специализации. Это может быть связано с различными способами использования одинаковых программных объектов. Следует также отметить, что все признаки, специализации и параметрические обобщения принадлежат множеству программных объектов X:

TМX и SМX.

Организация обобщающих параметрических процедур

Обобщающая параметрическая процедура F является отображением:

F: U₁ґU₂ ґ … ґU_nґZ₁ґZ₂ґ … ґZ_m ® Y₁ґY₂ґ … ґY_k,

где - U₁, U₂, …, U_n - параметрические аргументы, являющиеся параметрическими обобщениями, Z₁, Z₂, …, Z_m - прочие аргументы, Y₁, Y₂, …, Y_k - результаты отображения. Аргументы и результаты отображения принадлежат множеству X допустимых программных объектов: U_i О X, Z_j О X, Y_l О X.

Игнорируем особенности аргументов Z₁, Z₂, …, Z_m и результатов Y₁, Y₂, …, Y_k, обозначив их через W. Кроме того, нас будут интересовать не столько отображения, сколько параметрические аргументы. Тогда обобщающую параметрическую процедуру можно будет представить как:

F: U₁ґ U₂ґ …ґ U_nґ Z₁ґ Z₂ґ …ґ Z_m® Y₁ґ Y₂ґ …ґ Y_k є
є F: U₁ґ U₂ґ …ґ U_nґ Z₁ґ Z₂ґ …ґ Z_mґ Y₁ґ Y₂ґ …ґ Y_k є
є F: U₁ґ U₂ґ …ґ U_nґ W.

Сигнатуру обобщающей процедуры можно представить в обычной функциональной форме: F (U₁, U₂, … , U_n, W), где U₁, U₂, … , U_n - параметрические аргументы, а W - прочие аргументы и результаты. Для удобства восприятия параметрических аргументов предлагается записывать их отдельно от прочих аргументов, охватывая квадратными скобками:

F [U₁, U₂, … , U_n] (W) є F (U₁, U₂, … , U_n, W).

Наряду с разделением аргументов, такая запись подчеркивает один из возможных способов реализации механизма параметрического полиморфизма посредством многомерных массивов указателей на обработчики параметрических специализаций. Конструкцию [U₁, U₂, … , U_n] назовем параметрическим списком.

Основной задачей обобщающей параметрической процедуры является предоставление единого интерфейса для множества обработчиков параметрических специализаций. Обобщающая параметрическая процедура поддерживает выполнение следующих функций:

1. Обеспечивает доступ к требуемому обработчику параметрической специализации в зависимости от значения аргументов параметрического списка посредством параметрического полиморфизма. Реализация механизма доступа зависит от реализации параметрического обобщения и организации процесса обработки параметрических специализаций.
2. При необходимости, предоставляет обработчик параметрической специализации по умолчанию. Его можно использовать при отсутствии обработчика соответствующей специализации. Предоставление обработчика по умолчанию не является обязательным. В этом случае отсутствие обработчиков специализаций должно привести к выдаче ошибки во время компиляции, компоновки или выполнения. Момент выдачи такой ошибки определяется периодом окончательного формирования параметрического обобщения.
3. Обобщающая параметрическая процедура может предоставить и обработчик исключения, если отсутствует один из обработчиков специализации. Обработчик исключения можно использовать как во время компиляции, так и во время выполнения. Предполагается, что, при отсутствии обработчиков параметрических специализаций можно выбрать обработчик по умолчанию или обработчик исключения. Присутствие этих обработчиков предполагается определять опционально. Корректность логики функционирования программы при их отсутствии должна определяться средой разработки и исполнительной системой.

Организация обработчиков параметрических специализаций

Обработчики параметрических специализаций имеют сигнатуру, аналогичную сигнатуре обобщающей параметрической процедуры. Но они предназначены для обработки только определенных комбинаций значений параметрических аргументов. Комбинация, на которую "настроен" конкретный обработчик параметрической специализации, задается значениями признаков при описании его сигнатуры:

F[U₁(t_1i), U₂(t_2j), … , U_n(t_nk)] (X_m),

где t_qr О T_q - одно из значений признака, принадлежащего множеству признаков T_q параметрического обобщения U_q. Множество обработчиков некоторой обобщающей параметрической процедуры отличаются друг от друга тем, что каждый имеет уникальную комбинацию признаков, определяющую ту специализацию параметрического списка, которую он может обработать. Тело каждого обработчика содержит свой набор инструкций. Максимально возможное число обработчиков параметрических специализаций определяется как произведение мощностей признаков обобщений, входящих в параметрический список:

N = Ѕ T₁Ѕ ґ Ѕ T₂Ѕ ґ … ґ Ѕ T_nЅ ,

где T_i - множество признаков параметрического обобщения U_i.

При отсутствии обработчиков параметрических специализаций для некоторых комбинаций, их можно заменить обработчиком по умолчанию или обработчиком исключений.

Экземпляр параметрического обобщения

Экземпляром параметрического обобщения (параметрическим экземпляром) является размещаемый в памяти компьютера программный объект, для которого определено и зафиксировано одно из конкретных значений элемента отображения u_i = (t_i, S_j). При этом, во время работы программы, элемент S_j может принимать любое значение s_jqО S_j. Значение признака t_i в ходе вычислений должно оставаться неизменным.

Вызовы параметрических процедур

Вызовы параметрических процедур используются в ходе выполнения программы. Значения, подставляемые вместо списка формальных параметров, должны соответствовать сигнатуре обобщающей параметрической процедуры. В зависимости от значений признаков экземпляров параметрических обобщений, используемых в качестве фактических параметров, осуществляется выполнение тела соответствующей специализации. Вызов можно представить в следующей форме:

F [u_1i, u_2j, ... u_nk] (w_qr) ,

где [u_1i, u_2j, ... u_nk] - множество параметрических экземпляров, выступающих в роли аргументов параметрического списка; w_qr - прочие фактические параметры, передаваемые обработчику специализации.

При отсутствии обработчика специализации для подставляемого параметрического списка происходит вызов обработчика по умолчанию или запускается соответствующий обработчик исключения.

Что в результате?

Делая жалкую попытку формализации, я пытаюсь показать, что процедурно-параметрический механизм затрагивает только декларативную часть программы, определяющую модель состояния и интерфейс с моделью поведения. При этом, никоем образом не затрагивается сама модель поведения, располагаемая по другую сторону сигнатур. Это означает, что рассматриваемую надстройку можно использовать в различных алгоритмических моделях, а не только в процедурных языках. Она хорошо ложится на функциональное программирование, схемы потоков данных, различные модели параллельных вычислений, основанные на процессах, языки логического программирования.

Таким образом, я не вижу каких-либо технических причин, мешающих успешному становлению и развитию процедурно-параметрического программирования. За исключением, правда, несоответствия непосредственной метафоре объекта. Но это уже философия, а не программирование.

Подведение итогов

Поверхностные исследования процедурно-параметрической парадигмы программирования позволяют сделать следующие предварительные выводы.

1. Изучение возможностей модификации и эволюционного наращивания ПП программ, позволяет утверждать, что они практически ничем не уступают возможностям ОО подхода, а в ряде случаев и превосходят его.
2. Построение параметрических обобщений в целом соответствует восходящему проектированию. Это позволяет расширять существующий код путем повышения его универсальности, а не путем добавления специализаций, что присуще ОО подходу. Вместе с тем, не существует технических проблем для использования параметрических специализаций
3. Новые параметрические обобщения можно создавать на основе уже существующих обобщений, причем, самыми различными способами. Старые обобщения можно объединять включением, что позволяет создавать иерархические конфигурации, можно их сливать конкатенацией, используя при этом теоретико-множественные операции (объединение, пересечение разность и т.д.). При этом вновь разрабатываемые обобщающие параметрические процедуры могут использовать, в качестве своих параметрических специализаций, уже существующие обобщающие процедуры, построенные для реализации ранее существующих параметрических отношений.
4. Использование теоретико-множественных операций позволяет создавать ограниченные обобщения, скрывающие ряд специализированных процедур обработки. Это дает возможность создавать интерфейсы для различных клиентов с разными функциональными характеристиками без какого-либо переписывания методов. Такая возможность появляется из-за того, что манипуляция только данными может проходить более гибко по сравнению с манипуляцией объектами, содержащими еще и процедуры.
5. Одним из основных достоинств ППП является поддержка множественного полиморфизма, которая достигается использованием параметрического списка аргументов. Параметрический список задает многомерный массив отношений между различными специализациями, каждому вектору которого соответствует своя специализированная процедура. Это позволяет гибко модифицировать функциональные возможности программы, обеспечивающей взаимодействие между собой многих обобщенных объектов. ООП напрямую не поддерживает множественный полиморфизм.
6. Использование процедурно-параметрического подхода существенно повышает уровень унификации разработки. Повторно можно использовать ранее разработанные структуры данных и процедуры их обработки, создавая обобщения более высокого уровня. В принципе, ничто не мешает формировать обобщения на уровне уже готовых программ, если будут разработаны соответствующие инструменты, например, на основе языков сценариев.
7. Применение процедурно-параметрического подхода ведет к построению простых функциональных модулей нижнего уровня, предназначенных для выполнения специализированных задач в различном окружении. Эти модули могут обобщаться различными способами, в том числе, построением унифицированных модулей более высокого уровня. Стабильность низкоуровневых модулей снижает риск разработки более универсальных приложений.
8. Отсутствие непосредственной зависимости процедур от данных, присущей классам, позволяет формировать внешние интерфейсы независимо от привязки к внутренней структуре программных объектов. Одна и та же обобщающая параметрическая процедура может одновременно (через механизм ссылок) присутствовать в нескольких интерфейсах, каждый из которых предназначен для своей категории клиентов. Отсутствие привязки интерфейсов к организации процедур и данных позволяет гибко создавать и модифицировать программные компоненты.
9. Параметрическое обобщение позволяет объединять самые различные типы данных. Их совместное использование в качестве альтернатив происходит только при написании соответствующих процедур обработки. Такая возможность позволяет легко обобщать понятия, зависимость между которыми при первоначальном проектировании программы не была установлена. При этом не требуется изменения и повторного проектирования уже существующих механизмов.
10. Процедурно-параметрическая парадигма может использоваться совместно с объектно-ориентированным подходом. При этом последняя может осуществлять эволюционную специализацию программы сверху вниз, а первая - расширять ее обобщающие возможности снизу вверх. Кроме этого, методы классов можно расширять не только с использованием виртуализации, но и за счет параметризации.

Многие из представленных выводов не отражены в изложенном выше материале. Так что, мне еще есть, о чем писать.

Заключение

Представленная в работе процедурно-параметрическая парадигма программирования позволяет по-иному взглянуть на разработку сложных программных систем, их сопровождение, повторное использование и наращивание. На мой взгляд, эти проблемы могут решаться с не меньшей эффективностью, чем при использовании ОО подхода. Вместе с тем, ППП является развитием процедурного программирования и расширяет его полиморфизмом данных. Открываются новые пути дальнейших исследований и практических разработок, среди которых можно отметить следующие:

• разработка теоретического фундамента ППП;
• разработка методологии процедурно-параметрического проектирования и программирования;
• включение механизмов процедурно-параметрического полиморфизма, в существующие языки программирования;
• разработка новых языков, поддерживающих процедурно-параметрическое программирование;
• создание интегрированных средств разработки приложений, ориентированных на ППП;
• интеграция ППП с ООП (скрещивание ужа с ежом!?:).

На мой взгляд, повальное увлечение борьбой со сложностью, ориентированное на использование только ООМ, увлекло всех в одну сторону. Это привело к забвению альтернативных направлений исследований и разработок, позволяющих сформировать методы решения данной проблемы с использованием процедурного подхода. Процедурно-параметрическое программирование дает еще один шанс для дальнейшего развития уже подзабытых технологий.

Историческая справка

Началом ППП я считаю 0 часов с 13 на 14 января 2000 года. Да, да... именно Старый Новый год! Обстоятельства сложились так, что вместо традиционной рюмочки пришлось сесть за рабочий стол. Но я особо не сожалею, так как прошедшие праздники, связанные с встречей фиктивного тысячелетия и так подорвали мое здоровье. Поэтому, приступая к работе вечером 13-го с чувством вины за бесцельно пропитые дни, я, ложился спать ночью 14-го с уже сформированными терминами и достаточно четким представлением о том, что делать дальше.

В результате дальнейшей работы были написаны несколько документов для внутреннего использования (в связи с корявостью стиля и вульгарностью изложения), на основании которых сформировалась депонированная рукопись [Лег2000-1], являющаяся первоисточником идеи (хоть и с ошибками), и несколько статей, до сих пор находящихся в состоянии печати.

Так что, при наездах на мои измышления в печатных источниках, можете вставлять в список литературы следующие сведения:

Текст этой статьи, в упакованном виде уже лежит на моем сайте. После ознакомления с ним Вы, я думаю, поймете смысл посвящения. Именно с разбора простого алгоритма нахождения корней квадратного уравнения, при попытке решить несколько иную задачу, я и пришел к идее ПП парадигмы.

Не возражаю, если будет указан и сетевой адрес этого, более отработанного материала ( http://www.sofcraft.ru/paradigm/ppp/). Хотя, нет предела и его совершенству.

Нельзя сказать, что появление ППП было воспринято мною, как удар обухом по голове. С середины 90-х я ощущал недостатки ООП и даже пытался их исправить, предлагая различные расширения процедурного подхода [Легалов97-1, Легалов97-2]. Однако механизмы, рассматриваемые в этих статьях, были сырыми и не имели эффективного воплощения. Позднее я пытался разработать модель, объединяющую воедино механизмы конструирования, а также эквивалентного преобразования процедурных и объектных понятий [Легалов99]. Именно этой моделью я поначалу и занимался в ту праздничную ночь.

За прошедшие почти полтора года я не потерял интереса к развитию данной идеи, что наталкивает меня на мысль о ее жизнеспособности. Возможно, что я ошибаюсь. Или это уже было и оказалось бесплодным. Или это - полный бред. Поэтому с благодарностью восприму любые отклики, активизирующие процесс дальнейших размышлений.

А.Л.