[
содержание
| предыдущая тема
| следующая тема
]
Содержание темы
Необходимость использования автоматов с магазинной памятью. Организация автомата с магазинной памятью. Общая связь между грамматиками и автоматами с магазинной памятью. Связь между S-грамматикой и автоматом с магазинной памятью. Построение автомата с магазинной памятью по q-грамматике. LL(1) - грамматики Программная реализация нисходящего автомата с магазинной памятью.
Необходимость использования автоматов с магазинной памятью
Синтаксический разбор осуществляется с применением более сложных грамматик, обеспечивающих иерархическое определение одних правил через другие. Поэтому, для построения распознавателей, мощности конечных автоматов, используемых при лексическом анализе, уже не хватает. Необходим более мощный и универсальный автомат, поддерживающий построение дерева разбора и выстраивающий его как сверху вниз, так и снизу вверх. Из предыдущих тем известно, что конечный автомат можно расширить дополнительной рабочей памятью, чтобы обеспечить распознавание цепочек, порождаемых практически любыми грамматиками. Организация и поведение такого автомата определяется классом грамматик. Как определено в классификации Хомского, контекстно-свободным грамматикам можно поставить в соответствие автомат с магазинной памятью (АМП).
То, что даже простые цепочки проблематично распознать с использованием конечного автомата, можно проиллюстрировать решением следующей элементарной задачи: необходимо построить распознаватель правильной вложенности круглых скобок. Такая вложенность скобок часто встречается в различных языках программирования при построении арифметических выражений. Для решения данной задачи необходимо:
- определять равенство скобок, то есть количество открывающихся и закрывающихся скобок должно быть равным;
- следить за правильностью их вложения, то есть, чтобы любой закрывающейся скобке предшествовала соответствующая открывающаяся.
Невозможность использования конечного автомата подтверждается и тем, что грамматику, порождающую рассматриваемые цепочки, нельзя свести к праволинейной (тому виду, который, по классификации Хомского, эквивалентен конечному автомату). Ее также нельзя представить только итеративными диаграммами Вирта, непосредственно соответствующими конечному автомату. Это определяется наличием в грамматике правил с рекурсией в середине. А такая рекурсия не может быть сведена к итерации. Грамматика G7.1 Может быть определена следующим образом:
G7.1 = ({A, S}, { (, ) }, P, S) ,
Где P определяется как:
- S
 (A ) A (A ) A
- A
 S S
- A
 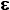
Одним из путей решения задачи является добавление счетчика скобок, который, при просмотре цепочки увеличивается на 1, если встретится открывающаяся скобка. Закрывающаяся скобка уменьшает значения счетчика на единицу. Начальное состояние счетчика (перед просмотром цепочки) равно 0. По завершении просмотра цепочки значение счетчика должно быть равным 0. При этом, в ходе просмотра цепочки счетчик не может принимать отрицательные значения. Подход обеспечивает решение поставленной задачи. Однако, наличие счетчика уже определяет автомат с дополнительно рабочей памятью, которому также необходимо наличие арифметического устройства. Поэтому, использование стека вряд ли будет сложнее. А экономить ячейки памяти мы давно уже разучились. Кроме того, в реальной ситуации могут быть более сложные зависимости. Например, может быть несколько видов скобок со своими правилами вложенности и их взаимным расположением. Значит, необходим универсальный подход, обеспечивающий преодоление различных ситуаций. Таким универсальным подходом и является использование автомата с магазинной памятью.
Организация автомата с магазинной памятью
АМП в качестве рабочей памяти использует стек, называемый также магазином. Данная память поддерживает только ограниченные операции доступа, в то же время достаточные для решения сложных задач, включая и задачи распознавания цепочек. Автомат с магазинной памятью определяется следующими пятью объектами:
- Конечным множеством входных символов, включающим концевой маркер (
 ). ).
- Конечным множеством магазинных символов, включающим маркер дна (
 ). ).
- Конечным множеством состояний, включающим начальное состояние.
- Устройством управления (УУ), которое каждой комбинации входного символа, магазинного символа и состояния ставит в соответствие выход или переход. Переход, в отличие от выхода, заключается в выполнении операций над магазином, состоянием и входом. Операции, запрашивающие входной символ после концевого маркера или выталкивания из магазина после маркера дна, а также операция вталкивания маркера дна, исключаются.
- Начальным содержимым магазина, содержащим маркер дна и, возможно пустую, цепочку магазинных символов.
Автомат с магазинной памятью называется распознавателем, если у него 2 выхода: "Допустить" и "Отвергнуть".
Операции автомата
Динамическое поведение АМП описывается через его операциями над входной цепочкой и стеком, а также переходами из одного состояния в другое. К операциям над стеком относятся:
- "Вытолкнуть" - выталкивает из стека верхний символ (будем также использовать сокращенное обозначение "
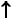 "). ").
- "Втолкнуть А" - вталкивает в стек магазинный символ А (будем также использовать сокращенное обозначение "
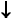 А"). А").
- "Заменить XYZ" - используется для сокращения записи, когда необходимо вытолкнуть верхний символ и вместо него втолкнуть несколько других (в данном случае X, Y, Z). Эквивалентна:
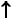  X X Y Y Z (сокращенно обозначим: Z (сокращенно обозначим:  XYZ). XYZ).
Переход АМП из одного состояния в другое указывается явно операцией "Состояние t", где t - новое состояние автомата (будем сокращать текст данной операции до "[t]").
Сдвиг входной головки на один символ вправо относительно входной ленты задается операцией "Сдвиг" (сократим до " "). После ее выполнения текущим символом становится следующий символ на входной ленте. Другой операцией над входной головкой является "Держать", которая не изменяет положение входной головки до следующего шага (можно просто не писать, если нет сдвига). "). После ее выполнения текущим символом становится следующий символ на входной ленте. Другой операцией над входной головкой является "Держать", которая не изменяет положение входной головки до следующего шага (можно просто не писать, если нет сдвига).
Переход или шаг автомата - это выполнение операций над стеком и входной головкой, а также изменение состояния. При этом необязательно, чтобы за один шаг происходили все изменения. Возможно: или входная головка останется на месте, или не произойдет операции над стеком, или не изменится состояние.
Распознаватель скобочных выражений
Рассмотрим одну из возможных реализация АМП, для задачи проверки корректности вложенности круглых скобок. Кратко опишем общий принцип работы автомата. Если входная головка читает "(", то в магазин заталкивается символ А. Если входная головка читает ")", то из магазина выталкивается содержащийся там символ. Цепочка отвергается, если:
- На входе остаются правые скобки, а магазин пуст.
- Входная цепочка прочитана до конца, а в магазине остаются символы А, соответствующие левым скобкам, для которых не нашлось пары.
Определим данный АМП следующим образом:
Множество входных символов: { (, ),  }. }.
Множество магазинных символов: { A,  } }
Множество состояний: t, где t является также и начальным состоянием автомата, раз оно единственное.
Переходы:
- (, A, S
  А, S, А, S, 
- (,
 , S , S   А, S, А, S, 
- ), A, S
  , S, , S, 
- ),
 , S , S  Отвергнуть Отвергнуть
 , A, S , A, S  Отвергнуть Отвергнуть , ,  , S , S  Допустить Допустить
В начальном состоянии магазин содержит только маркер дна ( ). ).
Из представленного описания видно, что поведение автомата имитирует ранее рассмотренный метод распознавания с использованием счетчика. Только вместо счетчика используются "палочки" (раньше с помощью палочек учили считать в школе). Эти палочки могут записываться в стек и стираться из него, отражая разность между прочитанными открывающимися и закрывающимися скобками. Работу данного АМП можно рассмотреть на примере распознавания нескольких цепочек. Пусть, первая цепочка будет иметь следующий вид:
( ( ) ( ) )
Тогда осуществляемые автоматом переходы можно представить в виде следующей последовательности текущих состояний его устройств.
|
Номер шага |
Содержимое стека |
Состояние автомата |
Остаток входной цепочки |
Номер
применяемого
правила |
|
1 |

|
[t] |
( ( ) ( ) )  |
2 |
|
2 |
 A A
|
[t] |
( ) ( ) )  |
1 |
|
3 |
 A A A A
|
[t] |
) ( ) )  |
3 |
|
4 |
 A A
|
[t] |
( ) )  |
1 |
|
5 |
 A A A A
|
[t] |
) )  |
3 |
|
6 |
 A A
|
[t] |
)  |
3 |
|
7 |

|
[t] |

|
Допустить |
В приведенном примере цепочка оказалась распознанной. Следующий пример раскрывает поведение автомата при распознавании цепочки, содержащей большее число правых круглых скобок чем левых:
( ) ) )
Таблица переходов и состояний в этом случае будет выглядеть следующим образом:
|
Номер шага |
Содержимое стека |
Состояние автомата |
Остаток входной цепочки |
Номер
применяемого
правила |
|
1 |

|
[t] |
( ) ) )  |
2 |
|
2 |
 A A
|
[t] |
) ) )  |
3 |
|
3 |

|
[t] |
) )  |
Отвергнуть |
Аналогичные таблицы можно представить и для других вариантов входных цепочек.
Устройство управления данного автомата с магазинной памятью можно представить в виде следующей таблицы переходов.
|
Магазинные
символы |
Входные символы |
|
( |
) |

|
|
A |
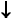 А, А, 
|
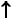 , , 
|
Отвергнуть |
|

|
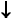 А, А, 
|
Отвергнуть |
Допустить |
Такая таблица является типичной формой представления одного внутреннего состояния для любого АМП. Если у автомата имеется несколько внутренних состояний, то для каждого из них строится такая таблица переходов. В большинстве реальных случаев АМП имеют только одно состояние.
Общая связь между грамматиками и автоматами с магазинной памятью
Эта связь давно доказана и рассмотрена в специальной литературе для различных классов грамматик и методов разбора. В рамках данной работы нет особой необходимости повторять материал или его выдержки из толстых книг. Можно только сослаться на основные источники информации, позволяющие получить фундаментальную подготовку по формальным грамматикам и методам разбора [Ахо78, Льюис]. Однако, и в этих книгах рассматриваются только такие грамматики и автоматы, которые могут быть эффективно реализованы. Из всего разнообразия грамматик, используемых для построения распознавателей, нас будут интересовать только КС(1) грамматики, ориентированные на нисходящий левый разбор, при котором входная цепочка просматривается слева направо. Использование данных грамматик позволяет создавать достаточно мощные и понятные языки программирования.
Следует пояснить, почему дальнейшее изучение ограничивается только нисходящими методами разбора. Методы, используемые при нисходящем разборе, достаточно универсальны и разнообразны. Применение восходящего разбора позволяет использовать более мощные KC(1) грамматики, в том числе и грамматики с левой рекурсией, которые при нисходящем разборе использовать невозможно. Возникают проблемы преобразования таких грамматик в грамматики с правой рекурсией, ориентированные на нисходящий разбор. Такое преобразование не всегда очевидно. Однако, применение диаграмм Вирта для представления синтаксиса языков программирования позволяет легко заменить все левые рекурсии на итерации и использовать полученные правила для нисходящего разбора. Поэтому, на мой взгляд, при практической разработке трансляторов, не имеет особого смысла использовать восходящий разбор. Забегая вперед, отмечу, что не вижу особого смысла использовать и автоматы с магазинной памятью, так как можно использовать другую модель распознавателя, более близкую по смыслу к диаграммам Вирта. Эта иерархически порождаемые конечные автоматы (пока я считаю, что для построения трансляторов она придумана и введена мною).
Для того, чтобы рассмотреть зависимость, существующую между КС(1) грамматиками и нисходящими распознавателями с магазинной памятью, обратимся к материалу, изложенному в книге Льюиса, Розенкранца и Стринза [Льюис]. Нет смысла выдумывать то, что уже изложено в виде, доступном для понимания.
Связь между S-грамматикой и автоматом с магазинной памятью
Не все КС-грамматики пригодны для построения нисходящего детерминированного АМП, так как многие из них могут порождать одну и ту же терминальную цепочку различными левыми выводами. Это говорит об их неоднозначности и невозможности использования для детерминированного разбора. Однако, определены и изучены такие классы грамматик, которые поддерживают нисходящий детерминированный разбор. Наиболее простыми из них являются S-грамматики.
КС-грамматика называется S-грамматикой (а также раздельной, или простой) тогда и только тогда, когда выполняются два условия:
- Правая часть каждого правила начинается терминалом Ti.
- Если два правила имеют совпадающие левые части, то правые части этих правил должны начинаться различными терминальными символами.
Пример
Рассмотрим две грамматики, которые задают один и тот же язык.
Грамматика G7.2(S), Содержит правила P:
- S
 aT aT
- S
 TbS TbS
- T
 bT bT
- T
 ba ba
Это не S-грамматика, так как правило 2 начинается с нетерминала, что нарушает условие 1, а правила 3, 4 имеют совпадающие левые части и начинаются с одинаковых терминальных символов.
S-грамматика G7.3(S) для этого же языка может использовать для порождения цепочек следующие правила:
- S
 abR abR
- S
 bRbS bRbS
- R
 a a
- R
 bR bR
Использование данной грамматики позволяет упростить разбор, используя для этого соответствующий АМП.
Обобщенный алгоритм построения нисходящего АМП для S - грамматики
Построение нисходящего автомата с магазинной памятью для заданной S-грамматики осуществляется по следующему обобщенному алгоритму.
- Множество входных символов автомата - это множество терминальных символов грамматики, расширенное концевым маркером.
- Множество магазинных символов состоит из маркера дна, нетерминальных символов грамматики и терминалов, встречающихся в правых частях правил, за исключением тех, которые занимают только крайнюю левую позицию.
- В начальном состоянии магазин содержит маркера дна и начальный нетерминал.
- Устройство управления АМП, имеет одно состояние и описывается управляющей таблицей, строки которой помечены магазинными символами, столбцы - входными символами, а элементы таблице описываются в ниже следующих пунктах.
- Каждому правилу грамматики ставится в соответствие элемент (клетка) таблицы. Правило должно иметь вид:
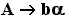 , ,
где А - нетерминал, b - терминал, 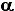 - цепочка из терминалов и нетерминалов. Этому правилу будет соответствовать элемент в строке А и столбце b: - цепочка из терминалов и нетерминалов. Этому правилу будет соответствовать элемент в строке А и столбце b:
Заменить (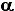 r), Сдвиг r), Сдвиг
где 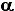 r - цепочка r - цепочка 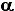 , записанная в обратном порядке (для того, чтобы удовлетворить соглашению, что верхний символ находится справа при принятом способе записи стека, когда его дно располагается слева). Если правило имеет вид , записанная в обратном порядке (для того, чтобы удовлетворить соглашению, что верхний символ находится справа при принятом способе записи стека, когда его дно располагается слева). Если правило имеет вид
А  b, b,
то вместо
Заменить 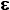 , Сдвиг , Сдвиг
используется
Вытолкнуть, Сдвиг.
- Если магазинным символом является терминал b, то элементом таблицы в строке b и столбце b будет
Вытолкнуть, Сдвиг
7. Элементом таблицы, который находится в строке маркера дна и столбце концевого маркера, является
Допустить
8. Элементы таблицы, не описанные ни в одном из пунктов 5, 6, 7 заполняются операцией
Отвергнуть
Используя данное описание, построим автомат для S- грамматики G7.3(S):
|
Магазинные
символы |
Входные символы |
|
a |
b |

|
|
S |
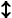 Rb, Rb, 
|
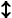 SbR, SbR,  
 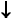 bR, bR, 
|
Отвергнуть |
|
R |
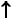 , , 
|
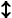 R, R, 
|
Отвергнуть |
|
b |
Отвергнуть |
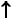 , , 
|
Отвергнуть |
|

|
Отвергнуть |
Отвергнуть |
Допустить |
Каким образом найдена представленная последовательность шагов построения АМП? Что-то получили с использованием дедукций, что-то - индукции. Остальное высосали из пальца. Если же присмотреться внимательнее к уже предложенным шагам, то можно понять, как они появились. В основе всего лежат особенности S-грамматики. Рассмотрим левый вывод терминальной цепочки bbababa. Он будет осуществляться следующим образом:
S  bRbS bRbS  bbRbS bbRbS  bbababR bbababR  bbababa bbababa
Процедура построения нисходящего дерева разбора, представленная на рис. 7.1, показывает, что на каждом шаге правило для дерева выбирается однозначно и увеличивает количество распознанных символов на один.
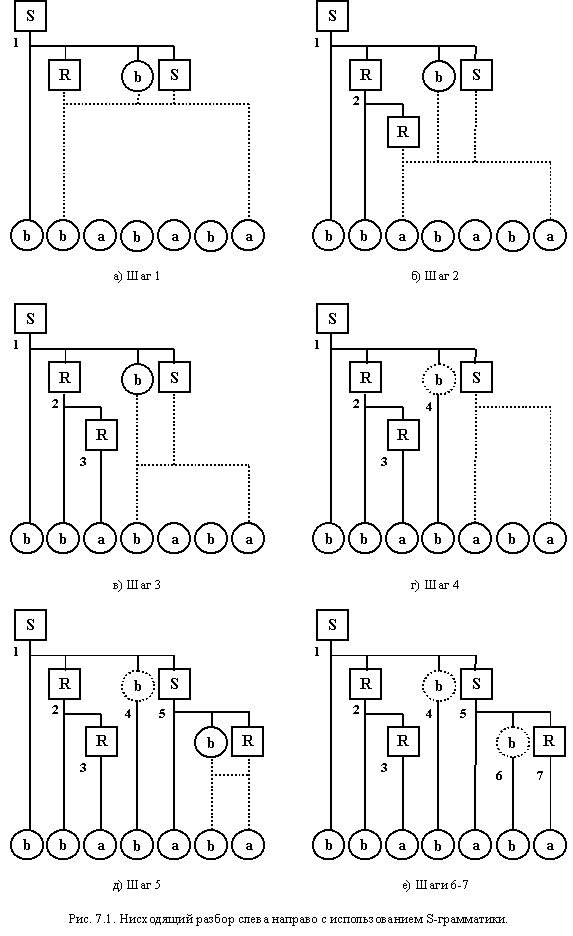
Этот выбор определяется грамматикой, которая четко устанавливает соответствие между текущим нетерминалом, входным символом, а также правилом, определяющим текущий нетерминал. Правило задано таким образом, что на первом месте в его правой части стоит символ, совпадающий с текущим символом цепочки. Поэтому, не нужны возвраты назад. Если соответствующего правила не будет найдено, произойдет отказ. При нахождении искомого правила, его первый символ нейтрализуется входным символом и отбрасывается (и потому не заносится в стек). Остальные же символы необходимо сохранить, чтобы использовать для формирования новых проверок на последующих шагах. Понятно также, что сохранение должно осуществляться в стеке (нет другой рабочей памяти) и в реверсивном порядке (так как самый левый символ правила должен разбираться первым, чтобы было соответствие с левым выводом). Отсюда также понятно, что терминалы, расположенные в середине правила, будут заноситься в стек и поэтому должны являться магазинными символами. Ясно также, что когда на вершине стека располагается терминал, он не может являться левой частью правила. Поэтому его необходимо просто вытолкнуть из стека, нейтрализуя эквивалентным входным символом.
S-грамматика и распознавание вложенности скобок
Обладая методами создания АМП по S-грамматике, вернемся к задаче распознавания вложенности скобок. Раньше соответствующий автомат был построен эвристически. Между тем, грамматика G7.1 не является S-грамматикой. И, к своему удивлению, мы не можем ее преобразовать к S-грамматике даже для этой простой задачи. Попытаемся разобраться с возникшими проблемами.
Нет ничего сложного в построении правила S-грамматики для начального нетерминала, правая часть которого всегда начинается с открывающейся скобки:
S  (B . (B .
Но, при определении B, возникает ряд проблем. Правая часть B может начинаться с закрывающейся скобки, за которой не будет следовать ничего:
B  ) . ) .
Но, вместе с тем, вслед за закрывающейся скобкой может вновь следовать произвольный набор вложенных скобок, полностью повторяющий цепочку, порождаемую из начального нетерминала:
B  )S . )S .
Возникает противоречие условию 2, которое в S-грамматике разрешить невозможно. Это противоречие не позволяет осуществить порождение произвольных цепочек. Остается только генерировать разнообразные варианты внутри охватывающих круглых скобок. Для этого правило B, начинающееся с открывающейся круглой скобки, должно выглядеть следующим образом:
B  (BB . (BB .
Данный анализ показывает, что вся проблема возникает из-за того, что предполагаемая цепочка может повториться множество раз или не появиться вообще (обобщая, можно сказать, что цепочка может повториться ноль или большее число раз). А возможность одновременного описания необязательных или повторяющихся цепочек как раз и отсутствует в S-грамматике. Для этих случаев необходимо иметь более мощный механизм порождения цепочек, допускающий пустые цепочки, например, q-грамматику.
Построение автомата с магазинной памятью по q-грамматике
Контекстно-свободная грамматика называется q-грамматикой тогда и только тогда, когда выполняются два условия:
1. Правая часть каждого правила либо представляет собой пустую цепочку ε, либо начинается с терминального символа.
2. Множество выбора правил с одной и той же левой частью не пересекаются.
Второе условие следует рассмотреть подробнее, так как необходимо ввести ряд определений. Одно из них - множество выбора. Для демонстрации определений будем использовать пример q-грамматики G7.4(S):
- S
 aAS aAS
- S
 b b
- A
 cAS cAS
- A
О том, что это не S - грамматика говорит правая часть правила 4, которая не начинается с терминального символа. Однако, метод построения НАМП, изложенный для S-грамматики почти подходит и здесь.
Множество терминалов, следующих за данным нетерминалом X (Обозначим через СЛЕД(X)) - множество терминальных символов, которые могут следовать непосредственно за Х в какой-либо промежуточной цепочке, выводимой из S , включая и , включая и  . .
Это множество символов называется также множеством следуемых за Х терминалов. Для приведенной грамматики можно определить следующие множества:
СЛЕД (А) = {a, b}
СЛЕД (S) = {a, b}
Терминалы, следующие за A, определяются исходя из того, что за A следует всегда нетерминал S, правая часть правила для которого начинается либо с a, либо с b. Терминалы, следующие за S, выводятся путем подстановки в правило 1 правила 3, которая показывает, что за S всегда следует S, начинающаяся либо с a, либо с b:
S  aAS aAS  acASS . acASS .
Данное понятие используется для того, чтобы показать, когда следует применять правило с пустой правой частью A  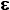 . Если входной символ Ti . Если входной символ Ti 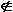 {a, b}, то есть, является символом c или {a, b}, то есть, является символом c или  , a на вершине магазина А, то бесполезно применять A , a на вершине магазина А, то бесполезно применять A  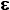 . Если это правило будет применено, то А удаляется из стека, а так как за А символы c или . Если это правило будет применено, то А удаляется из стека, а так как за А символы c или  следовать не могут, то в результате процесс останавливается. Представим, что у нас уже есть автомат, соответствующий грамматике G7.4, и очень похожий на АМП, распознающий S-грамматику. Тогда, применительно к цепочке аасbb, можно получить несколько решений. В начале рассмотрим стратегию, при которой в первую очередь применяется всегда пустое правило. следовать не могут, то в результате процесс останавливается. Представим, что у нас уже есть автомат, соответствующий грамматике G7.4, и очень похожий на АМП, распознающий S-грамматику. Тогда, применительно к цепочке аасbb, можно получить несколько решений. В начале рассмотрим стратегию, при которой в первую очередь применяется всегда пустое правило.
|
Номер шага |
Содержимое стека |
Остаток входной цепочки |
Номер
применяемого
правила |
Комментарии |
|
1 |
 S S
|
aacbb |
1 |
|
|
2 |
 SA SA
|
acbb |
4 |
Иначе, процесс разбора дальше не пойдет |
|
3 |
 S S
|
acbb |
1 |
|
|
4 |
 SA SA
|
cbb |
4 |
А здесь данный шаг ведет к отказу по отношению к правильной цепочке |
|
5 |
 S S
|
cbb |
Отвергнуть |
Придется осуществлять возврат |
Правильным было бы применение на шаге 4 правила 3, в соответствии с ранее рассмотренными рекомендациями о месте и времени применения пустого правила.
|
Номер шага |
Содержимое стека |
Остаток входной цепочки |
Номер
применяемого
правила |
Комментарии |
|
1 |
 S S
|
aacbb |
1 |
|
|
2 |
 SA SA
|
acbb |
4 |
Иначе, процесс разбора дальше не пойдет |
|
3 |
 S S
|
acbb |
1 |
|
|
4 |
 SA SA
|
cbb |
3 |
Пойдем в соответствии с предложенными рекомендациями |
|
5 |
 SSA SSA
|
bb |
4 |
Иначе, процесс разбора дальше не пойдет |
|
6 |
 SS SS
|
bb |
2 |
|
|
7 |
 S S
|
b |
2 |
|
|
8 |

|

|
Допустить |
Цепочка принадлежит языку! |
Таким способом решается одна из задач детерминированного разбора, связанная с особенностями применения пустого правила. Однако, при разборе, построенном на основе q-грамматики возможна и такая ситуация, когда:
A  b b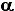 , A , A  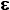 и b и b 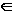 СЛЕД(A). СЛЕД(A).
В этом случае стоит проблема выбора одного из правил с одинаковыми левыми частями. Для ее решения введем понятие множества выбора для данного правила.
Если правило грамматики имеет вид: A  b b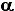 , где b - терминал, а , где b - терминал, а 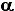 - цепочка терминалов и нетерминалов, то определим множество выбора для правила A → b - цепочка терминалов и нетерминалов, то определим множество выбора для правила A → b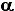 равным b. Обозначим данную запись следующим образом: равным b. Обозначим данную запись следующим образом:
ВЫБОР(A  b b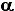 ) = b. ) = b.
Если правило имеет вид: A  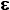 , то определим: , то определим:
ВЫБОР(A  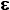 ) = СЛЕД(A). ) = СЛЕД(A).
Если p - номер правила, то будем также писать "ВЫБОР (p)" вместо "ВЫБОР (правило)"
ВЫБОР (p) - множество выбора правила p.
Проиллюстрируем построение множества выбора на примере грамматики G7.4.
ВЫБОР(1) = ВЫБОР (S  aAS) = {a} aAS) = {a}
ВЫБОР(2) = ВЫБОР (S  b) = {b} b) = {b}
ВЫБОР(3) = ВЫБОР (A  сAS) = {c} сAS) = {c}
ВЫБОР(4) = ВЫБОР (A  ε) = СЛЕД (A) = {a, b} ε) = СЛЕД (A) = {a, b}
В соответствии с определением, рассмотренным в начале, имеем q-грамматику, так как:
ВЫБОР(1)  ВЫБОР(2) = ВЫБОР(2) = 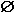 , ,
ВЫБОР(3)  ВЫБОР(4) = ВЫБОР(4) = 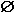 . .
Построение нисходящего автомата
Рассмотренные понятия и методы их использования приводят к небольшой корректировке правил порождения АМП по S-грамматике, чтобы получить процедуру создания автомата по q-грамматике. Эта корректировка касается только пункта 5. Можно, конечно, полностью переписать исправленный алгоритм создания автомата, тем более, что использование современных редакторов позволяет осуществить эту процедуру без проблем. К тому же компания Microsoft приучила нас не экономить ресурсы. Но я не буду оригинальным и воспользуюсь авторским текстом [Льюис]. Пятое правило заменяется двумя следующими:
5.1. Правило грамматики применяется всякий раз, когда магазинный символ является его левой частью, а входной символ принадлежит его множеству выбора. Для того, чтобы применить правило вида:
A  b b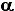 , ,
используется переход:
Заменить (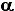 r), Сдвиг r), Сдвиг
Если правило имеет вид:
A  b, b,
то используется:
Вытолкнуть, Сдвиг.
Для того, чтобы применить правило:
A  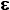
используется переход
Вытолкнуть.
5.2. Если имеется правило с нетерминалом A в левой части и элемент, соответствующий магазинному A и входному символу b не был создан по правилу 5.1., то таким элементом м.б. либо применение пустого правила (A  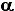 ) или операция "Отвергнуть". ) или операция "Отвергнуть".
Примеры построения АМП по q-грамматике
Построим автомат с магазинной памятью по q-грамматике, используемой выше для различных иллюстраций. Его таблица переходов будет иметь следующий вид.
|
Магазинные
символы |
Входные символы |
|
a |
b |
c |

|
|
S |
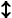 SA, SA, 
|
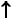 , , 
|
Отвергнуть |
Отвергнуть |
|
A |
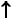
|
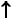
|
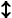 SA, SA, 
|
Отвергнуть |
|

|
Отвергнуть |
Отвергнуть |
Отвергнуть |
Допустить |
Следующий пример иллюстрирует использование правила 5.2, когда описанное в нем ячейка таблицы переходов может быть реализована любым из двух вариантов. Я бы предпочел второй, чтобы меньше мучиться. Грамматика G7.5(S) описывается следующими правилами:
1. S  aA aA
2. S  b b
3. A  cSa cSa
4. A  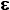
Множества выбора для каждого из правил будут выглядеть следующим образом:
ВЫБОР(1) = ВЫБОР (S  aA) = {a} aA) = {a}
ВЫБОР(2) = ВЫБОР (S  b) = {b} b) = {b}
ВЫБОР(3) = ВЫБОР (A  сSa) = {c} сSa) = {c}
ВЫБОР(4) = ВЫБОР (A  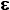 ) = СЛЕД (A) = {a, ) = СЛЕД (A) = {a,  } }
Полученные данные использованы для построения таблицы переходов. Ячейка, содержащая альтернативные правила, находится на пересечении строки с магазинным символом A и столбце с входным символом b.
|
Магазинные
символы |
Входные символы |
|
a |
b |
c |

|
|
S |
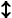 A, A, 
|
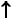 , , 
|
Отвергнуть |
Отвергнуть |
|
A |
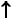
|
1)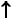 или 2)Отвергнуть или 2)Отвергнуть |
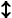 aS, aS, 
|
|
|
a |
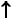 , , 
|
Отвергнуть |
Отвергнуть |
Отвергнуть |
|

|
Отвергнуть |
Отвергнуть |
Отвергнуть |
Допустить |
Для того, чтобы проверить, как действуют эти правила, необходимо ввести неправильную цепочку. Возьмем для примера цепочку ab. В первом случае используем выталкивание, которое ведет к отвержению цепочки на третьем шаге.
|
Номер шага |
Содержимое стека |
Остаток входной цепочки |
Применяемый переход |
Комментарий |
|
1 |
 S S
|
ab |
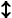 A, A, 
|
|
|
2 |
 A A
|
b |
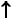
|
Использовано выталкивание |
|
3 |

|
b |
Отвергнуть |
Все равно отвергли |
Во втором варианте цепочка отвергается уже на втором шаге.
|
Номер шага |
Содержимое стека |
Остаток входной цепочки |
Применяемый переход |
Комментарий |
|
1 |
 S S
|
ab |
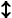 A, A, 
|
|
|
2 |
 A A
|
b |
Отвергнуть |
На шаг раньше |
Распознавание вложенности скобок и q-грамматика
Теперь у нас достаточно знаний для построения простой грамматики, порождающей вложенные скобки. Данная q-грамматика содержит следующие правила:
- S
 (B)B (B)B
- B
 (B)B (B)B
- B
 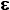
Правила выбора выглядят следующим образом:
ВЫБОР(1) = ВЫБОР (S  (B)B ) = {(} (B)B ) = {(}
ВЫБОР(2) = ВЫБОР (B  (B)B ) = {(} (B)B ) = {(}
ВЫБОР(3) = ВЫБОР (B  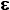 ) = СЛЕД (B) = {), ) = СЛЕД (B) = {),  } }
Они лишний раз подтверждают, что мы построили q-грамматику. Следует специально отметить, что, начиная с q-грамматики, далее постоянно приходиться доказывать принадлежность грамматики заданному классу, чтобы затем использовать необходимые процедуры построения автомата. Таблица переходов данного автомата будет выглядеть следующим образом:
|
Магазинные символы |
Входные символы |
|
( |
) |

|
|
S |
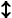 B)B, B)B, 
|
Отвергнуть |
Отвергнуть |
|
B |
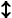 B)B, B)B, 
|
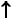
|
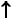
|
|
) |
Отвергнуть |
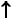 , , 
|
Отвергнуть |
|

|
Отвергнуть |
Отвергнуть |
Допустить |
LL(1) - грамматики
Понятие множества выбора можно обобщить таким образом, чтобы применять его к КС-грамматикам произвольного вида.
LL(1)-грамматика - это такая КС(1)-грамматика, в которой множества выбора правил с одинаковыми левыми частями не пересекаются.
Обобщение понятия множества выбора позволяет использовать правила, начинающиеся с нетерминалов. В качестве примера можно представить LL(1)-грамматику, содержащую следующие правила:
- S
 AbB AbB
- S
 d d
- A
 Cab Cab
- A
 B B
- B
 cSd cSd
- B
 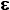
- C
 a a
- C
 ed ed
То, что это LL(1)-грамматика, еще надо доказать, так как в противном случае результат разбора может оказаться непредсказуемым. Да и автомат с магазинной памятью мы построить не сможем из-за того, что не имеем дополнительной информации, требуемой для построения таблицы переходов. А она появляется в ходе доказательств.
В книге Льюиса и пр. [Льюис] приводится описание доказательства принадлежности заданной грамматики к LL(1)-грамматике. Оно занимает одиннадцать страниц, использует демонстрационные примеры, разреженные матрицы и т.д. Я неоднократно принимался за его чтение, но каждый раз с грустью убеждался, что мой IQ (надо как-нибудь, хоть разок, проверить его значение) является недостаточно высоким, чтобы осилить материал. Поэтому были попытки перескочить эти страницы, выбросить нисходящий разбор из головы и обратиться к другой религии, проповедующей восходящий разбор. Но и здесь мне не хватило веры в истинность избранного пути. Поэтому, как это часто бывает в жизни, я нашел одну маленькую религию, которую подогнал под свои воззрения. После этого я смог не только успокоить свою душу, но и нести новый свет в массы. Эта религия зиждется на диаграммах Вирта, источая дальше свои идеи на распознаватели и реализацию. Подробно она будет раскрыта в следующей теме. Ее применение позволило обойти мне непереваримое доказательство и остаться в лоне нисходящего разбора.
Программная реализация нисходящего автомата с магазинной памятью
Разработку программы, реализующей логику работы нисходящего распознавателя, можно осуществить на основе построенной таблицы переходов нисходящего автомата с магазинной памятью. Кроме того, учитывая эквивалентность построенной таблицы, и исходной грамматики, а также используя особенности организации современных языков программирования, можно осуществить реализацию на основе имеющихся правил. Главное в этом случае, чтобы грамматика соответствовала одному из рассмотренных классов (изучайте пропущенное доказательство). Метод разработки программы на основе синтаксических правил называется рекурсивным спуском.
Разработка программы по таблице переходов АМП
В этом случае нам необходимо построить наборы магазинных и входных символов, смоделировать основные устройства автомата и написать процедуру, реализующую таблицу переходов. Основными модулями являются стек и модуль чтения входной цепочки символов.
Реализация стека должна, по крайней мере поддерживать три основных функции: вталкивание в стек (Push), выталкивание из стека (Pop) и чтение вершины стека (Top). Стек должен контролировать возможное переполнение и попытку выталкивания маркера дна (маркер явно может отсутствовать, поэтому необходимо контролировать попытку выталкивания из пустого стека).
Модуль чтения входной цепочки содержит набор функций, обеспечивающих доступ к требуемому входному потоку, а также перемещение по нему слева направо.
Таблица переходов может быть реализована с использованием переключателей (например, операторов switch в языках C, C++) или путем интерпретации данных, располагаемых в соответствующей матрице. Второй способ позволяет строить различные распознаватели, не меняя программу, а первый работает намного быстрее.
Чтобы не быть голословными, схематически рассмотрим один из вариантов возможной реализации на примере, распознавателя круглых скобок. При этом, учитывая учебный характер примера, будем придерживаться простейших структур данных и постараемся обойтись без лишних проверок. Принятые при реализации решения кратко описаны в виде комментариев к разрабатываемой программе, исходный текст которой приводится ниже. Программа реализует таблицу переходов с применением переключателей. Для упрощения разработки строка скобок читается с клавиатуры.
// BrackStack.cpp - автомат с магазинной памятью,
// распознающий вложенность круглых скобок.
// Построен на основе таблицы переходов,
// созданной по следующей q-грамматике:
// 1. S -> (B)B
// 2. B -> (B)B
// 3. B -> empty
#include <iostream>
#include <string>
#include <vector>
#include <stack>
using namespace std;
// Магазинными символами автомата являются:
// S, B, маркер дна (bottom).
// Их значение должно быть за пределами видимых символов.
enum stackSymb {S = 256, B, bottom};
// Строка с входной цепочкой, имитирующая входную ленту
string str;
int i; // Текущее положение входной головки
stack <int, vector<int> > stck; // Стек для магазинных символов
// Функция, реализующая чтение символов в буфер из входного потока.
// Используется для ввода с клавиатуры распознаваемой строки.
// Ввод осуществляется до нажатия на клавишу Enter.
// Символ '\n' яляется концевым маркером входной строки.
void GetOneLine(istream &is, string &str) {
char ch;
str = "";
for(;;) {
is.get(ch);
if(is.fail() || ch == '\n') break;
str += ch;
}
str += '\n'; // Добавляется концевой маркер
}
// Инициализация устройств АМП
void Init() {
// Инициализация стека
while(!stck.empty()) stck.pop();
stck.push(bottom);
stck.push(S);
// Инициализация входной головки
i = 0;
}
// Устройство управления АМП, анализирующего вложенность скобок.
// Имитирует таблицу переходов АМП.
bool Parser() {
// Инициализация устройств АМП
Init();
int step = 0;
// Цикл анализа состояний
for(;;) {
// Тестовый вывод информации о текущем шаге,
// текущем символе, вершине стека
cout <<"step " << step++ << ": str[" << i << "] = "<< str[i]
<< " Top = "<< stck.top() << "\n";
// Проверка содержимого на вершине стека
switch(stck.top()) {
// Анализ первой строки таблицы переходов
case S:
switch(str[i]) {
case '(': // [S, (]
stck.top() = B; // эквивалентно stck.pop(); stck.push(B);
stck.push(')');
stck.push(B);
i++; // следующий входной символ
break;
case ')': // [S, )] - ) не может стоять в начале
cout << "Position " << i << ", "
<< "Error 1: \')\' can not is in begin!\n";
return false;
case '\n': // [S, концевой маркер]
cout << "Position " << i << ", "
<< "Error 2: Empty string!\n";
return false;
default: // Ошибка, такой символ не допустим
cout << "Position " << i << ", "
<< "Incorrect symbol! " << str[i] << "\n";
return false;
}
break;
// Анализ второй строки таблицы переходов
case B:
switch(str[i]) {
case '(': // [B, (]
stck.top() = B; // эквивалентно stck.pop(); stck.push(B);
stck.push(')');
stck.push(B);
i++; // следующий входной символ
break;
case ')': // [B, )] - вытолкнуть без сдвига
stck.pop();
break;
case '\n': // [B, концевой маркер] - вытолкнуть без сдвига
stck.pop();
break;
default: // Ошибка, такой символ не допустим
cout << "Position " << i << ", "
<< "Incorrect symbol! " << str[i] << "\n";
return false;
}
break;
// Анализ третьей строки таблицы переходов
case ')':
switch(str[i]) {
case '(': // [), (] - в принципе недостижимо
cout << "Position " << i << ", "
<< "Error 3: I want \')\'!\n";
return false;
case ')': // [), )] - вытолкнуть со сдвигом
stck.pop(); // вытолкнуть
i++; // сдвиг
break;
case '\n': // [), концевой маркер]
cout << "Position " << i
<< ", Error 4: I want \')\'!\n";
return false;
default: // Ошибка, такой символ не допустим
cout << "Position " << i << ", "
<< "Incorrect symbol! " << str[i] << "\n";
return false;
}
break;
// Анализ четвертой строки таблицы переходов
case bottom:
switch(str[i]) {
case '(': // [bottom, (] - невозможно при пустом магазине
cout << "Position " << i << ", "
<< "Error 4: Impossible situation [bottom, \'(\']!\n";
return false;
case ')': // [bottom, )] - лишняя )
cout << "Position " << i << ", "
<< "Error 5: unnecessary \')\'!\n";
return false;
case '\n': // [bottom, концевой маркер] - допустить!
return true;
default: // Ошибка, такой символ не допустим
cout << "Position " << i << ", "
<< "Incorrect symbol! " << str[i] << "\n";
return false;
}
break;
}
}
}
// Главная функция используется для инициализации устройств
// АМП перед каждым новым прогоном и тестирования до тех пор,
// пока не будет прочитана пустая строка.
int main () {
string strCursor;
str = "";
// Цикл распознавания различных входных цепочек
do {
// Чтение очередной входной цепочки в буфер
cout << "Input bracket\'s expression!: ";
// Формируем очередную строку скобок для распознавания.
GetOneLine(cin, str);
// Здесь начинается разбор принятой строки.
if(Parser())
cout << "+++++ OK! +++++\n";
else
cout << "--- Fatal error (look upper error message)! ---\n";
// Вывод разобранной строки и значения позиции входой головки.
cout << "Line: " << str;
strCursor = " Pos: " + string(i, '-');
strCursor +='^';
cout << strCursor << " i = " << i << "\n\n";
} while(str != "\n");
cout << "Goodbye!\n";
return 1;
}
Исходные тексты распознавателей на C++, C# и Go можно скачать с сайта. Помимо этого можно посмотреть работу распознавателя на основе автомата с магазинной памятью, написанного на JavaScript или скачать соответствующие исходники.
Разработка программы с использованием метода рекурсивного спуска
Метод рекурсивного спуска учитывает особенности современных языков программирования, в которых реализован рекурсивный вызов процедур. Если обратиться к дереву нисходящего разбора слева направо (рис. 7.1), то можно заметить, что в начале происходит анализ всех поддеревьев, принадлежащих самому левому нетерминалу. Затем, когда самым левым становится другой нетерминал, то анализ происходит для него. При этом используются и полностью раскрываются все нижележащие правила. Это навязывает определенные ассоциации с иерархическим вызовом процедур в программе, следующих друг за другом в охватывающей их процедуре. Поэтому, все нетерминалы можно заменить соответствующими им процедурами или функциями, внутри которых вызовы других процедур - нетерминалов и проверки терминальных символов будут происходить в последовательности, соответствующей их расположению в правилах. Такая возможность подкрепляется и другой ассоциацией. Вызов процедуры или функции реализуется через занесение локальных данных в стек, который поддерживается системными средствами. Заносимые данные определяют состояние обрабатываемого нетерминала, а машинный стек соответствует магазину автомата.
Использование рекурсивного спуска позволяет достаточно
быстро и наглядно писать программу распознавателя на основе имеющейся грамматики.
Главное, чтобы последняя соответствовала требуемому виду. Исходный текст
программы распознавания вложенности скобок, использующей метод рекурсивного
спуска, приведен ниже. Несмотря на наличие совпадающих функций, программа
приведена полностью, чтобы дать отчетливое представление об ее структуре.
// Рекурсивный распознаватель вложенности круглых скобок.
// Построен на основе правил следующей q-грамматики:
// 1. S -> (B)B
// 2. B -> (B)B
// 3. B -> empty
#include <iostream>
#include <string>
#include <vector>
#include <stack>
using namespace std;
// Строка с входной цепочкой, имитирующая входную ленту
string str;
int i; // Текущее положение входной головки
int erFlag; // Флаг, фиксирующий наличие ошибок в середине правила
// Функция, реализующая чтение символов в буфер из входного потока.
// Используется для ввода с клавиатуры распознаваемой строки.
// Ввод осуществляется до нажатия на клавишу Enter.
// Символ '\n' яляется концевым маркером входной строки.
void GetOneLine(istream &is, string &str) {
char ch;
str = "";
for(;;) {
is.get(ch);
if(is.fail() || ch == '\n') break;
str += ch;
}
str += '\n'; // Добавляется концевой маркер
}
// Функция, реализующая распознавание нетерминала B.
bool B() {
if(str[i] == '(') {
i++;
if(B()) {
if(str[i] == ')') {
i++;
if(B()) { // Если последний нетерминал корректен,
// то корректно и все правило.
return true;
} else { // Ошибка в нетерминале B
erFlag++;
cout << "Position " << i << ", "
<< "Error 1: Incorrect last B!\n";
return false;
}
} else { // Это не ')'
erFlag++;
cout << "Position " << i << ", "
<< "Error 2: I want \')\'!\n";
return false;
}
} else {
erFlag++;
cout << "Position " << i << ", "
<< "Error 3: Incorrect first B!\n";
return false;
}
} else // Смотрим другую альтернативу:
return true; // Пустая цепочка допустима
}
// Функция, реализующая распознавание нетерминала S.
bool S() {
if(str[i] == '(') {
i++;
if(B()) {
if(str[i] == ')') {
i++;
if(B()) {
if(str[i] == '\n') {
return true; // за последним нетерминалом - конец
} else { // Там ничего не должно быть
erFlag++;
cout << "Position " << i << ", "
<< "Error 4: I want string end after last right bracket!\n";
return false;
}
} else {
erFlag++;
cout << "Position " << i << ", "
<< "Error 4: Incorrect last B!\n";
return false;
}
} else {
erFlag++;
cout << "Position " << i << ", "
<< "Error 5: I want \')\'!\n";
return false;
}
} else {
erFlag++;
cout << "Position " << i << ", "
<< "Error 6: Incorrect first B!\n";
return false;
}
}
return false; // Первый символ цепочки некорректен
// то, что это ошибка, лучше определить снаружи
}
// Функция запускающая разбор и определяющая корректность его завершения,
// если первый символ не принадлежит цепочки
bool Parser() {
// Начальная инициализация.
erFlag = 0;
i = 0;
// Процесс пошел!
if(S())
return true; // Все прошло нормально
else {
if(erFlag)
cout << "Position " << i << ", "
<< "Error 7: Internal Error!\n";
else
cout << "Position " << i << ", "
<< "Error 8: Incorrect first symbol of S!\n";
return false; // Есть ошибки
}
}
// Главная функция используется для тестирования до тех пор,
// пока не будет прочитана пустая строка
int main () {
string strCursor;
str = "";
// Цикл распознавания различных входных цепочек
do {
// Чтение очередной входной цепочки в буфер
cout << "Input bracket\'s expression!: ";
// Формируем очередную строку скобок для распознавания.
GetOneLine(cin, str);
// Здесь начинается разбор принятой строки.
if(Parser())
cout << "+++++ OK! +++++\n";
else
cout << "----- Fatal error (look upper error message)! -----\n";
// Вывод разобранной строки и значения позиции входой головки.
cout << "Line: " << str;
strCursor = " Pos: " + string(i, '-');
strCursor +='^';
cout << strCursor << " i = " << i << "\n\n";
} while(str != "\n");
cout << "Goodbye!\n";
return 1;
}
Исходные тексты данного примера на C++, C# и Go также доступны для скачивания. Помимо этого можно посмотреть работу распознавателя, написанного на JavaScript или скачать соответствующие исходники.
Следует отметить, что две представленные программы отличаются только фрагментами, осуществляющими разбор. Тестовая функция у них совпадает. Трудно сказать, какой из методов лучше. Использование рекурсивного спуска позволяет написать программу быстрее, так как не надо строить автомат. Ее текст может быть и менее ступенчатым, если использовать инверсные условия проверки или другие методы компоновки текста. Лично я не вижу причин заменять рекурсивный спуск автоматом с магазинной памятью, особенно в том случае, если грамматику задавать с использованием диаграмм Вирта. Но в общем (в который раз!) можно сказать, что о вкусах не спорят.
Контрольные вопросы и задания
- Зачем, при синтаксическом разборе нужны автоматы с магазинной памятью?
- Как организован автомат с магазинной памятью?
- Основные операции автомата с магазинной памятью.
- Каким образом ограничения, накладываемые на грамматику, определяют реализацию автомата?
- Приведите примеры известных Вам ограниченных грамматик.
- Каким образом можно построить АМП по s-грамматике?
- Недостатки S-грамматики.
- Разработка АМП по q-грамматике.
- Приведите определения и краткие характеристики S-, q-, L-грамматик.
- Методы программной реализации нисходящих автоматов с магазинной памятью.
- Какие возможны варианты программной реализации нисходящего распознавателя при непосредственном использовании таблицы переходов АМП?
- В чем специфика распознавателя, построенного с применением рекурсивного спуска?
[
содержание
| предыдущая тема
| следующая тема
]
|