[
содержание
| предыдущая тема
| следующая тема
]
Содержание темы
Семантический разрыв между формальными грамматиками и автоматами с магазинной памятью. Модель динамически порождаемых конечных автоматов. Графический метаязык для описания динамически порождаемых конечных автоматов. Использование диаграмм Вирта для представления динамически порождаемых конечных автоматов, распознающих КС(1) грамматику.
Примечание. Возможно, что представленный ниже материал для большинства не покажется полезным с практической точки зрения. Но хотелось подвести хоть какое-то обоснование под используемые методы и практические приемы разработки трансляторов. При наличии представления о нескольких десятках языков программирования и более чем о десятке формальных моделей постоянно возникают маниакальные идеи разработать "супер"
язык или модель. Для меня эта модель не является ни первой, ни последней. А.Л.
Семантический разрыв между формальными грамматиками и автоматами с магазинной памятью
Применение автоматов с магазинной памятью для построения нисходящих распознавателей показывает, что одним из препятствий на пути эффективной разработки трансляторов является семантический разрыв [Майерс]
между формальным описанием исходных языков и методами реализации трансляторов этих языков. Семантический разрыв проявляется в том, что объекты и операции, которыми разработчик манипулирует при описании языка, не совпадают с объектами и операциями, которыми разработчику приходится манипулировать при реализации транслятора.
Обобщенно, процесс построения типичного транслятора выглядит следующим образом:
- разработка синтаксиса (формального описания) языка;
- разработка распознавателя языка на основе полученного формального описания.
Описание синтаксиса осуществляется с использованием формальной грамматики, которая определяет синтаксическую структуру языка. Построение же распознавателя основывается на автоматной модели и оперирует соответствующими понятиями из теории автоматов, такими, как входной алфавит автомата, множество его состояний, множество магазинных символов и переходов.
Наличие семантического разрыва приводит к необходимости преодолевать ряд проблем в при разработке транслятора. Первая из них -
необходимость преобразования модели формальной грамматики в автоматную модель распознавателя. Между этими моделями существует несколько противоречий:
- Противоречие между иерархической структурой исходного описания языка с использованием формальной грамматики и одноуровневой табличной моделью автомата, реализующего синтаксический разбор.
Формальные грамматики оперирует абстрактными понятиями, заложенными в основу языка, такими как программа,
тип или арифметическое выражение. Все описание языка можно рассматривать как набор понятий, связанных между собой некоторыми отношениями. Для представления этих понятий в метаязыках используется нетерминальные символы. Одни нетерминалы могут описываться через другие, более мелкие, формируя, таким образом, некоторую структуру взаимосвязей между понятиями языка. Описание одного нетерминала может состоять из нескольких правил, но эти правила всегда рассматриваются вместе. В противоположность этому, автомат с магазинной памятью, построенный на основе формальной грамматики, оперирует понятиями магазинных символов, некоторые из которых могут соответствовать понятиям языка (нетерминалам исходной грамматики). Однако большинство из них представляют собой не имеющие смысла для разработчика компилятора языка символы, появившиеся в результате преобразования модели формальной грамматики к модели автомата с магазинной памятью, которыми, тем не менее, разработчик вынужден манипулировать. Таким образом, при построении автомата теряется исходная структура правил языка. Кроме того, структурированность описания часто исчезает за счет вынужденного разложения единственного правила, описывающего некоторый нетерминал. Это разложение преобразует грамматику к виду, удобному для построения автомата с магазинной памятью. В результате, в процессе работы с преобразованной моделью, разработчик вынужден постоянно держать в уме исходную структуру понятий языка, что чревато большой вероятностью внесения в проект ошибок.
- Противоречие между высокоуровневыми средствами описания языков и ограничениями на грамматики, используемые для перехода к автоматной модели распознавателя.
Все современные метаязыки позволяют разработчику использовать относительно высокоуровневые механизмы, такие как альтернативные фрагменты правил, итерации и необязательные конструкции. Вместе с тем, на грамматику, из которой может быть получен искомый автомат с магазинной памятью, накладываются жесткие ограничения, касающиеся непосредственно вида ее правил, и эти ограничения не допускают использование описанных выше механизмов.
Формальное описание языка, в конечном счете, должно быть преобразовано в модель автомата, осуществляющего разбор. Это преобразование основывается на эвристических алгоритмах, каждый из которых ориентирован на конкретный класс грамматик и автоматов. В результате необходимости применения данного шага теряется связь между исходным описанием языка и его реализацией. Если в процессе разработки будут внесены изменения в автоматную модель, то они уже никаким образом не повлияют на исходное представление, которое часто является также и пользовательским описанием.
Вторая проблема -
это необходимость преобразования грамматики. Для преобразования исходного описания языка в соответствующую автоматную модель, необходимо, чтобы грамматика принадлежала какому-либо конкретному классу. Если это условие не выполняется, то автомат не может быть реализован, и, следовательно, требуется преобразование грамматики. Если выясняется, что грамматика языка требует преобразования, то это может означать что:
- язык принадлежит требуемому классу, то есть существует грамматика, описывающая его и обладающая необходимыми признаками;
- язык не принадлежит требуемому классу, и любые попытки преобразования грамматики обречены на неудачу.
Первая ситуация возникает, если реализация языка не представляет трудностей, но при попытке его описания была использована грамматика, не удовлетворяющая необходимым условиям. В этом случае исходная грамматика может быть преобразована в допустимую, хотя это не является идеальным подходом. Дело в том, что в большинстве случаев преобразования приходится выполнять вручную разработчику компилятора, используя при этом эвристические приемы, каждый из которых ориентирован на конкретный класс грамматики. Существуют причины, по которым желательно избегать таких преобразований. Во-
первых, трудно выбрать вид преобразования, во-вторых, невозможно гарантировать, что они не изменят создаваемый язык.
Вторая ситуация может возникнуть, когда описываемый язык сложен и содержит конструкции, которые могут представлять затруднения при их разборе. Попытка описания этих конструкций языка на синтаксическом уровне приводит к тому, что изначально описываемый язык не будет удовлетворять требованиям, допускающим его реализацию. Естественно, что любая грамматика этого языка не будет удовлетворять налагаемым условиям, и все попытки получения допустимой грамматики потерпят неудачу.
Модель динамически порождаемых конечных автоматов
Для сокращения семантического разрыва предлагается модель динамически порождаемых конечных автоматов. Описание исходного языка с использованием данной модели, с одной стороны, сохраняет описанные выше и свойственные современным метаязыкам иерархичность и высокий уровень представления, а с другой, не требует преобразования в плоскую (одноуровневую) автоматную модель распознавателя, так как может быть реализована непосредственно в терминах используемых абстракций.
Обычный конечный автомат позволяет описывать только регулярные конструкции языков. Предлагаемая модель расширяет конечный автомат и позволяет описывать любой контекстно-свободный язык.
Динамически порождаемый конечный автомат (ДПК-автомат) - это четверка:
S = (A, Z, 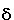 , u1), , u1),
где:
- A = { a1, ..., as, ..., aS } - множество всех состояний автомата (алфавит состояний); as
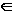 (U (U  V), где U = { u1, ..., um, ..., uM } - множество основных состояний, V = { v1, ..., vn, ..., vN } - множество зарезервированных конечных состояний автомата, U V), где U = { u1, ..., um, ..., uM } - множество основных состояний, V = { v1, ..., vn, ..., vN } - множество зарезервированных конечных состояний автомата, U  V = V = 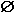 ; ;
- Z = { z1, ..., zf, ..., zF } - множество входных символов (входной алфавит); zf
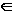 (T (T  G), где T = { t1, ..., tk, ..., tK } - множество терминальных символов, G = { g1, ..., gp, ..., gP } - множество порождающих символов, T G), где T = { t1, ..., tk, ..., tK } - множество терминальных символов, G = { g1, ..., gp, ..., gP } - множество порождающих символов, T  G = G = 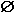 ; ;
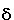 : U : U 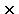 Z Z 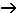 A - функция переходов, реализующая отображение G в A; функция A - функция переходов, реализующая отображение G в A; функция 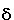 некоторым парам основное состояние - входной символ (um, zf) ставит в соответствие состояние автомата as = некоторым парам основное состояние - входной символ (um, zf) ставит в соответствие состояние автомата as = 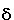 (um, zf), as (um, zf), as 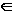 A; A;- u1
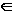 U - начальное состояние автомата. U - начальное состояние автомата.
Распознаватель языка R = {Si } i=1...T - это множество динамически порождаемых конечных автоматов. Автомат S1, используемый для инициализации процесса распознавания, называется начальным.
В исходный момент ДПК-автомат находится в состоянии u0. При переходе в одно из зарезервированных конечных состояний vn автомат завершает свою работу, возвращая логическое значение, определяемое этим состоянием. Возможны три конечных состояния и соответствующие им значения, которые приведены в таблице 1. Возвращаемое значение используется при динамическом порождении автоматов.
Таблица 1
Множество зарезервированных конечных состояний
|
Обозначение |
Название |
Возвращаемое значение |
|
v1 |
допуск |
Истина |
|
v2 |
откат |
Ложь |
|
v3 |
ошибка |
Ложь |
Входной алфавит Z ДПК-автомата объединяет два множества. Множество терминальных символов T - это символы алфавита описываемого языка, поступающие на вход автомата непосредственно из входного потока. Каждому символу gp из множества порождающих символов G соответствует свой конечный автомат Si, входящий в состав распознавателя языка, то есть 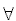 gp gp 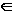 G G 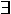 Si Si 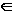 R. Порождающий символ gp служит условным обозначением тех подцепочек символов во входной цепочке, которые могут быть распознаны ДПК-автоматом Si, соответствующим данному порождающему символу. R. Порождающий символ gp служит условным обозначением тех подцепочек символов во входной цепочке, которые могут быть распознаны ДПК-автоматом Si, соответствующим данному порождающему символу.
Переход автомата в основное состояние um, по порождающему символу gi, вызывает динамическое порождение экземпляра соответствующего ДПК-автомата Si, который производит попытку распознавания текущей подцепочки. Возвращаемые порожденным автоматом логическое значение и результат сравнения текущего входного символа с терминальными символами входной цепочки, определяют срабатывание того или иного перехода в новое состояние. В общем случае возможно одновременное срабатывание нескольких переходов, но тогда полученная модель автомата не будет являться детерминированной. Поэтому в разработанную автоматную модель введен механизм приоритетов срабатывания переходов. В соответствии с этим механизмом для каждого состояния um пары (um, zf), f = 1,...,F упорядочены в порядке проверки срабатывания соответствующих им переходов.
Описание языка представляет собой совокупность динамически порождаемых автоматов, каждый из которых описывает одно из понятий, определяющее синтаксис языка.
Графический метаязык для описания динамически порождаемых конечных автоматов
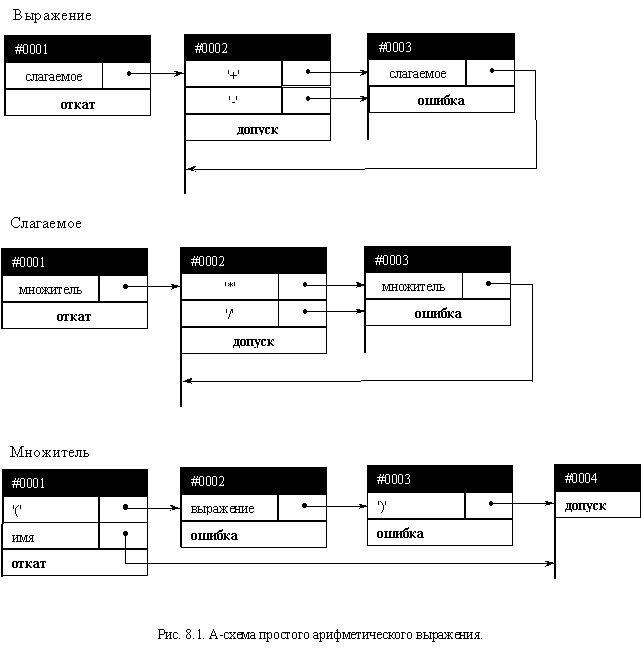
Для визуального представления предлагаемой модели описания разработан графический метаязык (А-схемы), отображающий модель ДПК-автомата в виде ориентированного размеченного графа, вершины которого соответствуют состояниям автомата, а связи между вершинами - переходам. В качестве примеров описания грамматик с использованием этого метаязыка на рис. 8.1 приведено описание синтаксиса простейших арифметических выражений.
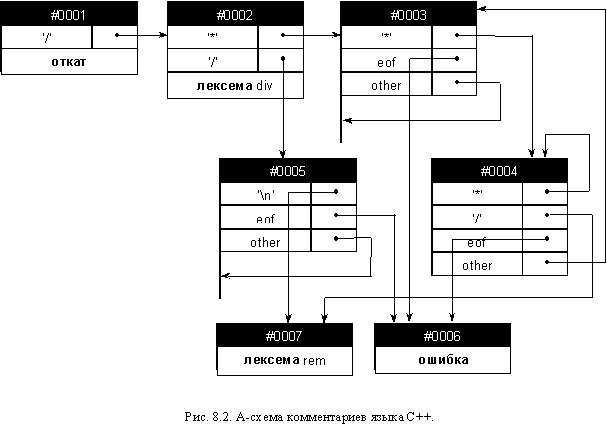
На рис. 8.2 - описание синтаксиса комментариев языка С++.
Ниже перечислены несколько основных принципов, которые были заложены в основу метаязыка.
- Каждое состояние автомата um представляется в виде вершины, состоящей из заголовка и последующих нескольких строк. Каждая строка соответствует переходу автомата и может иметь две различные формы представления. В первом случае строка содержит один из символов входного алфавита zf, по которому может быть выполнен переход, и начальную точку, из которой проводится соответствующая ветвь перехода. Такая строка соответствует паре текущее состояние - входной символ (um, zf), которой функция δ ставит в соответствие некоторое новое состояние as. Строки, соответствующие парам (um, zf), располагаются в порядке убывания приоритета сопоставленных им переходов. Во втором случае строка содержит название одного из зарезервированных конечных состояний vn, вызывающих завершение работы автомата. Эта строка является сокращенной формой записи перехода в указанное конечное состояние, если не был выполнен ни один из переходов, сопоставленных предыдущим строкам вершины. Такая строка должна быть последней строкой вершины автомата.
- Номер m состояния автомата отображается в заголовке состояния. Можно также задавать имена тем состояниям, которые имеют осмысленную интерпретацию. В этом случае вместо номера состояния в заголовке отображается его имя.
- Каждое состояние автомата отображается с утолщенной левой границей, которая может быть продолжена за пределы исходной вершины. Эта линия и заголовок состояния предназначены для связывания состояний между собой через ветви переходов. Ветвь перехода берет начало из начальной точки, расположенной в соответствующей строке перехода, и оканчивается на заголовке или левой границе того состояния, в которое требуется перейти. Использование специальным образом выделенных начальных и конечных точек переходов позволяет использовать ветви в виде простых линий без стрелок на концах.
- С каждой строкой перехода может быть связана некоторая семантика, для доступа к которой используются интерактивные возможности среды разработки, в которую предполагается интегрировать данный метаязык.
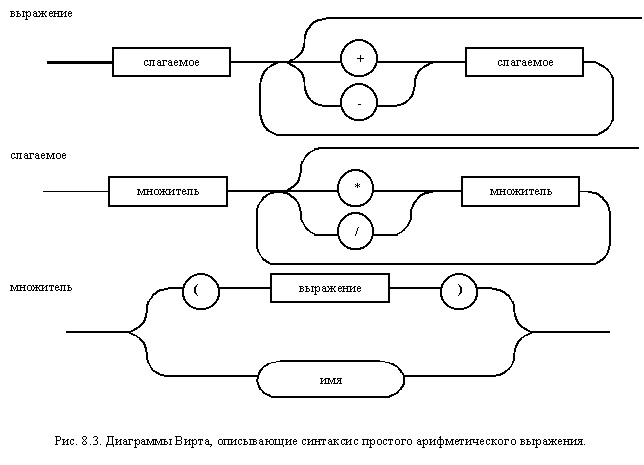
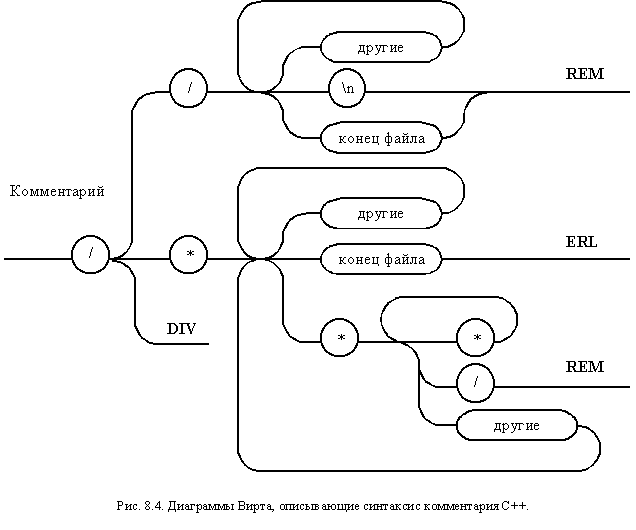
Метаязыком, наиболее близким к А-схемам, являются диаграммы Вирта и R-схемы. Можно легко построить алгоритмы преобразования между ними. Ниже перечислены действия, необходимые для преобразования диаграмм Вирта к А-схемам.
- Диаграмма Вирта, описывающая нетерминал преобразуется в А-схему, описывающую соответствующий ДПК-автомат.
- Вершины диаграммы Вирта соответствуют ветвям перехода между состояниями автомата.
- Множества исходящих альтернативных связей диаграммы Вирта, образующие точки ветвления, соответствуют состояниям ДПК-автомата. Точки входа и выхода из графа диаграммы Вирта соответствуют начальному и конечному состояниям ДПК-автомата.
Диаграммы Вирта, соответствующие ранее представленным А-схемам выражения и комментария, приведены на рис. 8.3 и 8.4 соответственно.
Примечание. К сожалению (а может, к счастью:) все дальнейшие работы по созданию инструментальной системы на основе этого метаязыка оказались замороженными. Сказалась нехватка времени и других ресурсов. А так хотелось слепить графическую альтернативу yacc'у и lex'у! Что делать?! Не я первый, не я последний. А.Л.
Использование диаграмм Вирта для представления динамически порождаемых конечных автоматов, распознающих КС(1) грамматику
Из представленных примеров видно, что диаграммы Вирта можно непосредственно использовать не только в качестве метаязыка для представления формальных грамматик, но и как язык представления динамически порождаемых конечных автоматов. При этом, отдельным автоматом будет являться любое из правил уже разработанного синтаксиса языка программирования. Такой подход позволяет использовать диаграммы Вирта для построения нисходящего распознавателя точно так же, как они использовались для построения лексических анализаторов. Основным отличием от лексического анализа является то, что диаграммы распознавателя содержат нетерминалы, которые обрабатываются отдельными, динамически порождаемыми конечными автоматами.
Применение другой автоматной модели позволяет интерпретировать процесс нисходящего распознавания с использованием диаграмм Вирта следующим образом.
- Каждая диаграмма Вирта задает один динамически порождаемый конечный автомат.
- Входными символами любого динамически порождаемого конечного автомата являются терминальные символы, поступающие из входной цепочки и нетерминалы, определяющие отдельные правила.
- Начальным состоянием динамически порождаемого автомата является входная дуга диаграммы Вирта.
- Конечному состоянию автомата соответствует выходная дуга диаграммы Вирта.
- Множество состояний любого динамически порождаемого конечного автомата является множество точек ветвления связей диаграммы Вирта, описывающих различные альтернативы ветвления. При наличии только одной альтернативы состоянию автомата соответствует дуга, выходящая из терминальной или нетерминальной вершины.
- Процесс распознавания начинается с порождения автомата, задаваемого правилом, описывающим начальный нетерминал.
- Проход через терминальную вершину соответствует переходу по символу входной цепочки определяемому в этой вершине. При этом осуществляется переход из одного состояния автомата в другое.
- Проход через нетерминальную вершину соответствует динамическому порождению нового конечного автомата в соответствии с именем нетерминала и продолжением разбора из его начального состояния.
- Достижение конечного состояния эквивалентно достижению выхода диаграммы Вирта. В этом случае автомат сигнализирует об успешном завершении работы сигналом "допустить", который передается породившему его автомату. Родительский автомат считает в этом случае проведенный разбор нетерминал успешным и переходит в следующее состояние в соответствии с дугой выходящей на диаграмме Вирта из разобранного нетерминала.
- Если автомат не может перейти из начального состояния в следующее, он порождает сигнал "отката" и передает управление своему родительскому автомату. Родительский автомат, получив данный сигнал, пытается осуществить анализ другой существующей альтернативы.
- При невозможности перехода в другое состояние из состояния, не являющегося начальным, автомат сигнализирует об ошибки выдачей сигнала "отказ". Это ведет к отказу входной цепочки и завершению работы всех автоматов.
- Цепочка допускается в том случае, если ее допускает автомат, порожденный для распознавания начального нетерминала.
Контрольные вопросы и задания
- В чем заключается семантический разрыв между грамматиками и автоматами с магазинной памятью?
- Определите модель динамически порождаемых конечных автоматов.
- Взаимосвязь между ДПК-автоматами и диаграммами Вирта.
[
содержание
| предыдущая тема
| следующая тема
]
|